#1 알고리즘
#1-1

문제의 조건 자체는 쉽지만, 테스트 케이스가 아주 많다. 따라서 빨리 계산해야 한다. 그렇게 하기 위해서 비트 연산을 이용한다. 먼저, 십진수로 값이 0인 변수를 선언하고, 그 변수에 0비트가 20개 있다고 친다. 오른쪽에서부터 n번째 자리에 있는 비트가 n이 '집합'에 존재하는지의 유무를 표시한다고 생각한다. 1이면 존재하고, 0이면 존재하지 않는다.
#1-2
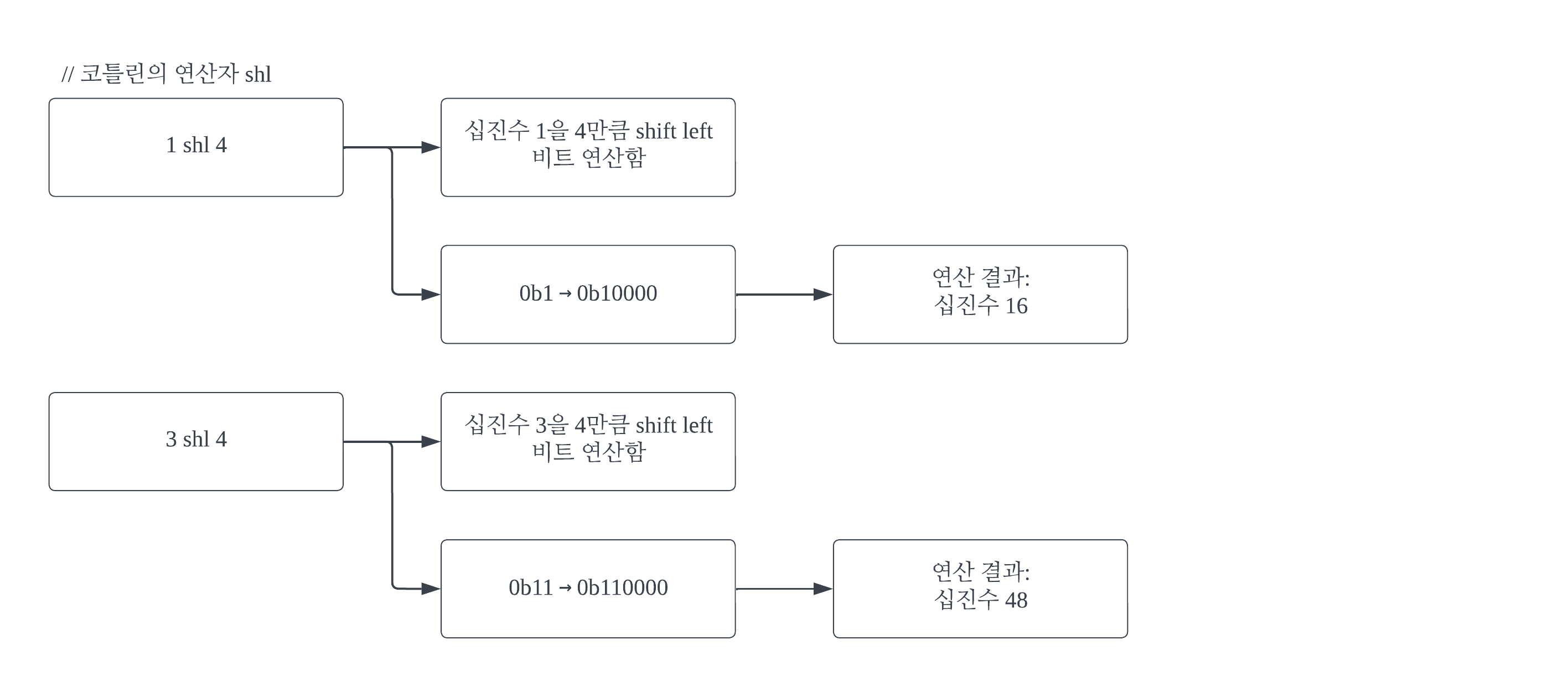
이 문제의 풀이를 위해 주요하게 사용할 비트 연산은 << 연산 (left shift 연산)이다. 코틀린에서는 해당 연산을 shl라는 연산자로 지원한다. 1 shl a는 2진법으로 (a + 1)번째 자리가 1이고 나머지는 0인 수를 도출한다. 따라서 (1 shl (a - 1))로 a라는 값을 가지는 수가 '집합'에 존재함을 나타낼 수 있다.
#2 코드 - 코틀린
import java.io.BufferedReader
import java.io.InputStreamReader
import java.io.BufferedWriter
import java.io.OutputStreamWriter
val br = BufferedReader(InputStreamReader(System.`in`))
val bw = BufferedWriter(OutputStreamWriter(System.out))
var bits : Int = 0 // 0 == 0b00000000000000000000
fun main() {
for(i : Int in 0..<br.readLine().toInt()) {
val command = br.readLine()
when(command[1]) { // 2번째 글자
'd' -> commandAdd(command.substring(4).toInt())
'e' -> commandRemove(command.substring(7).toInt())
'h' -> commandCheck(command.substring(6).toInt())
'o' -> commandToggle(command.substring(7).toInt())
'l' -> commandAll()
'm' -> commandEmpty()
else -> continue
}
}
br.close()
bw.flush()
bw.close()
}
fun commandAdd(x: Int) {
/* x가 3이라면, 1 shl (x - 1)는
* 0b00000000000000000100
*/
bits = bits or (1 shl (x - 1))
}
fun commandRemove(x: Int) {
/* x가 3이라면, (1 shl (x - 1)).inv()는
* 0b11111111111111111011
*/
bits = bits and (1 shl (x - 1)).inv() // inv()는 모든 비트를 반전시킨다.
}
fun commandCheck(x: Int) {
if(bits and (1 shl (x - 1)) == 0) { // bits의 x번째 자리가 1이 아니라면
bw.write("0\n")
} else {
bw.write("1\n")
}
}
fun commandToggle(x: Int) {
bits = bits xor (1 shl (x - 1))
}
fun commandAll() {
bits = 0b11111111111111111111
}
fun commandEmpty() {
bits = 0
}'문제 풀이 ✏️ > 기타' 카테고리의 다른 글
| [백준] 2579 (계단 오르기) (0) | 2023.12.27 |
|---|---|
| [백준] 2606 (바이러스) (0) | 2023.12.26 |
| [백준] 2108 (통계학) (0) | 2023.12.15 |
| [백준] 28417 (스케이트보드) (0) | 2023.12.11 |
| [백준] 11866 (요세푸스 문제 0) (0) | 2023.12.09 |