#1 알고리즘
#1-1

힙(heap)이라는 영어 단어의 사전적 의미는 쌓아 놓은 무더기다. 그리고 이 단어는 프로그래밍에서도 사용된다. 첫째로 메모리 영역에서, 둘째로 자료구조에서다. 이 둘은 서로 다른 개념이지만, 힙(heap)이라는 단어를 쓴 만큼 각각 힙의 사전적 의미와 관련된 내용이 있다. 메모리 영역에서의 힙은 무더기라는 뉘앙스를 풍긴다. 프로그램 수행 도중 그 크기가 변하지 않는 정적 할당과 달리 동적 할당은 필요한 만큼 크기가 무더기로 증가할 수 있기 때문이다. 자료구조에서의 힙은 '무더기'기 보단, 쌓임이라는 의미가 강조된다. 노드가 특정한 규칙을 지키며 차곡차곡 쌓이는 모습에서 힙이라는 이름이 붙었다.
#1-2
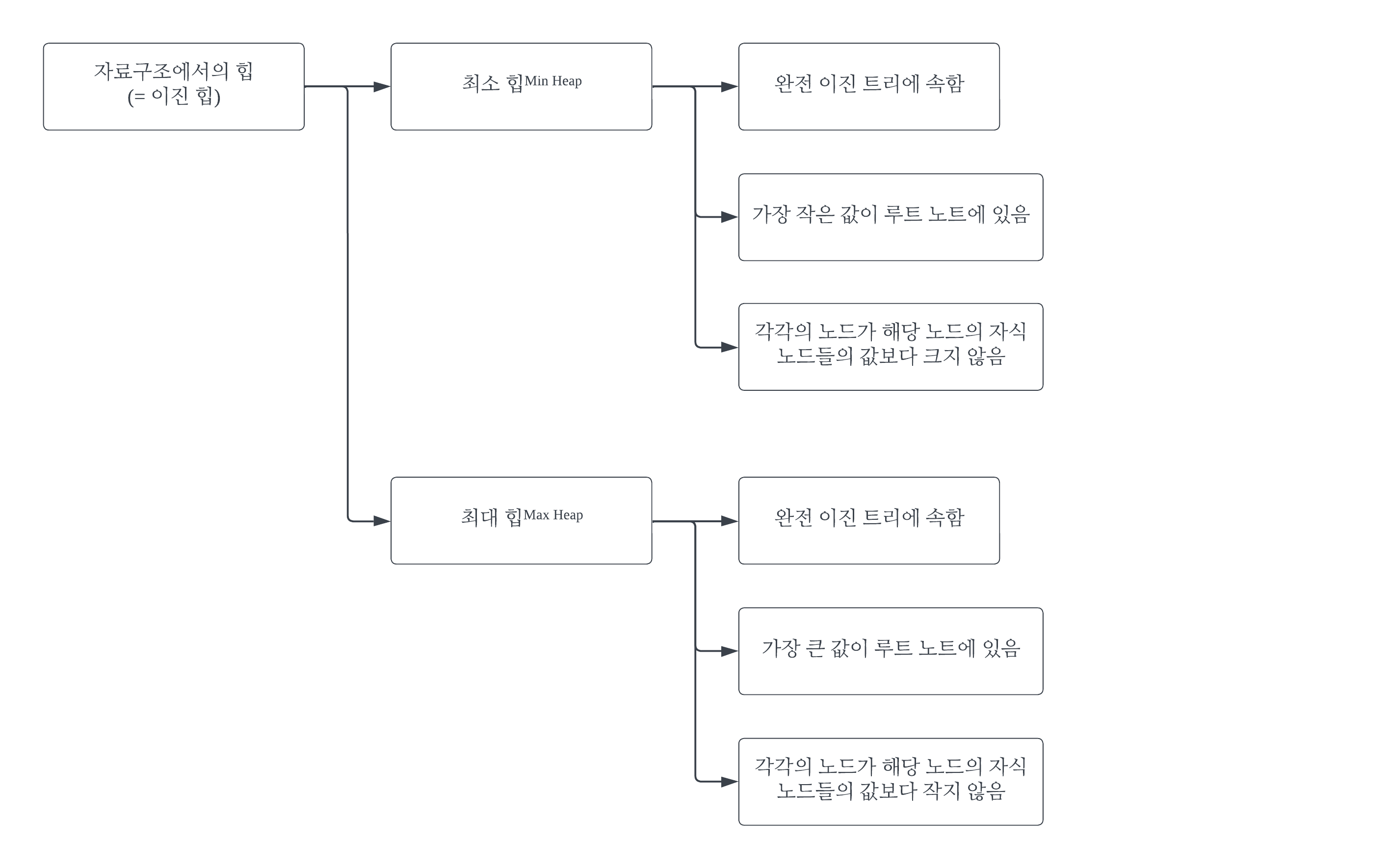
힙 정렬은 자료구조에서의 힙을 이용하는 정렬이다. 자료구조에서의 힙은 최소 힙과 최대 힙 2가지 종류가 있다. 힙 정렬은 두 힙 중 어느 것을 사용해도 된다. 이 글에서는 최소 힙을 이용해 힙 정렬을 수행한다.
#1-3
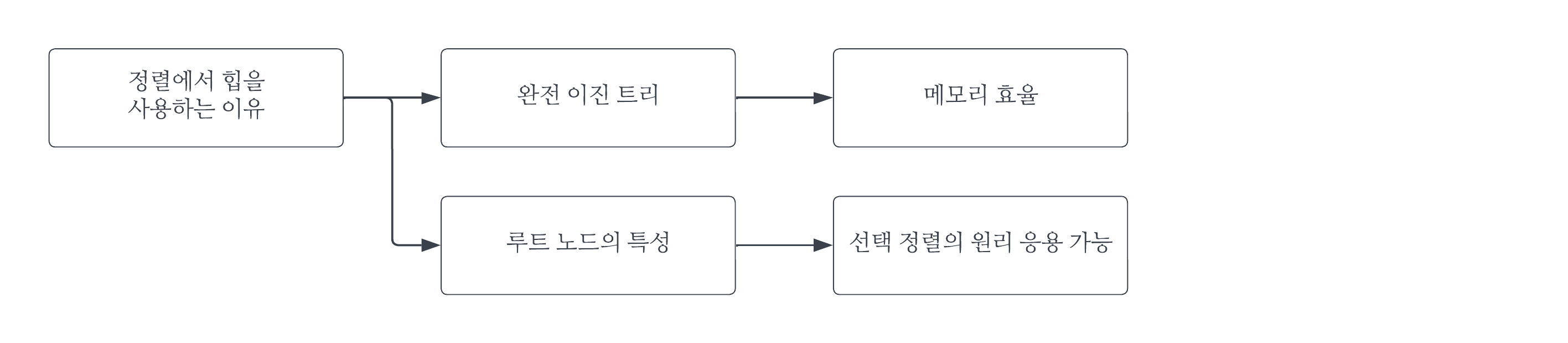
힙 정렬을 본격적으로 설명하기 앞서, 힙을 이용해서 정렬할 수 있는 이유가 무엇인지 짚고 넘어간다. 그것은 힙이 가진 2가지 특성 덕분이다. 첫째로 힙은 완전 이진 트리로, 불완전 이진 트리 대비 정보가 없는 빈 공간이 없다. 따라서, 메모리 공간을 효율적으로 사용할 수 있다. 둘째로 이진 힙은 루트 노드가 항상 최솟값(최소 힙) 또는 최댓값(최대 힙)을 가진다. 그렇기에, 선택 정렬의 원리(값 하나를 '선택'해서, 뒤쪽에 차곡차곡 쌓음)를 응용할 수 있다.
#1-4
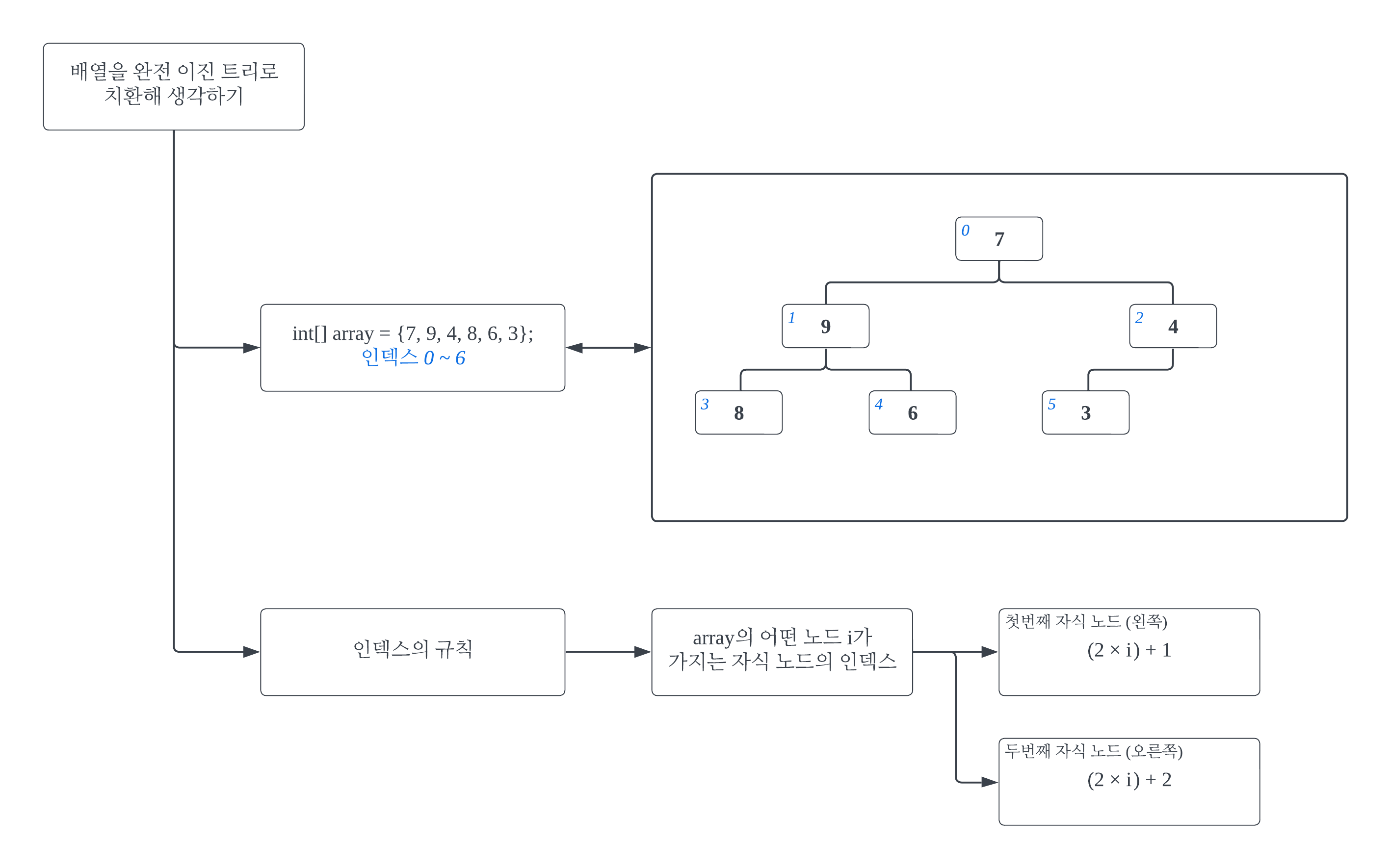
완전 이진 트리는 다음과 같이 배열로 치환해 생각할 수 있고, 반대 방향으로도 가능하다. 힙 정렬 알고리즘에서는 주어진 배열을 완전 이진 트리로 치환해 생각한다.
#1-5

완전 이진 트리를 이진 힙으로 다듬는 것을 수선이라고 표현한다. 이진 힙의 2종류 '최소 힙'과 '최대 힙' 중에서, 최소 힙을 이용하기로 한다. 따라서, heapify() 수행 후의 array[0]는 항상 최솟값이다. 이걸 maxIndex로 보내면 과정을 반복하면, 결과적으로 array는 내림차순으로 정렬된다.
#1-6
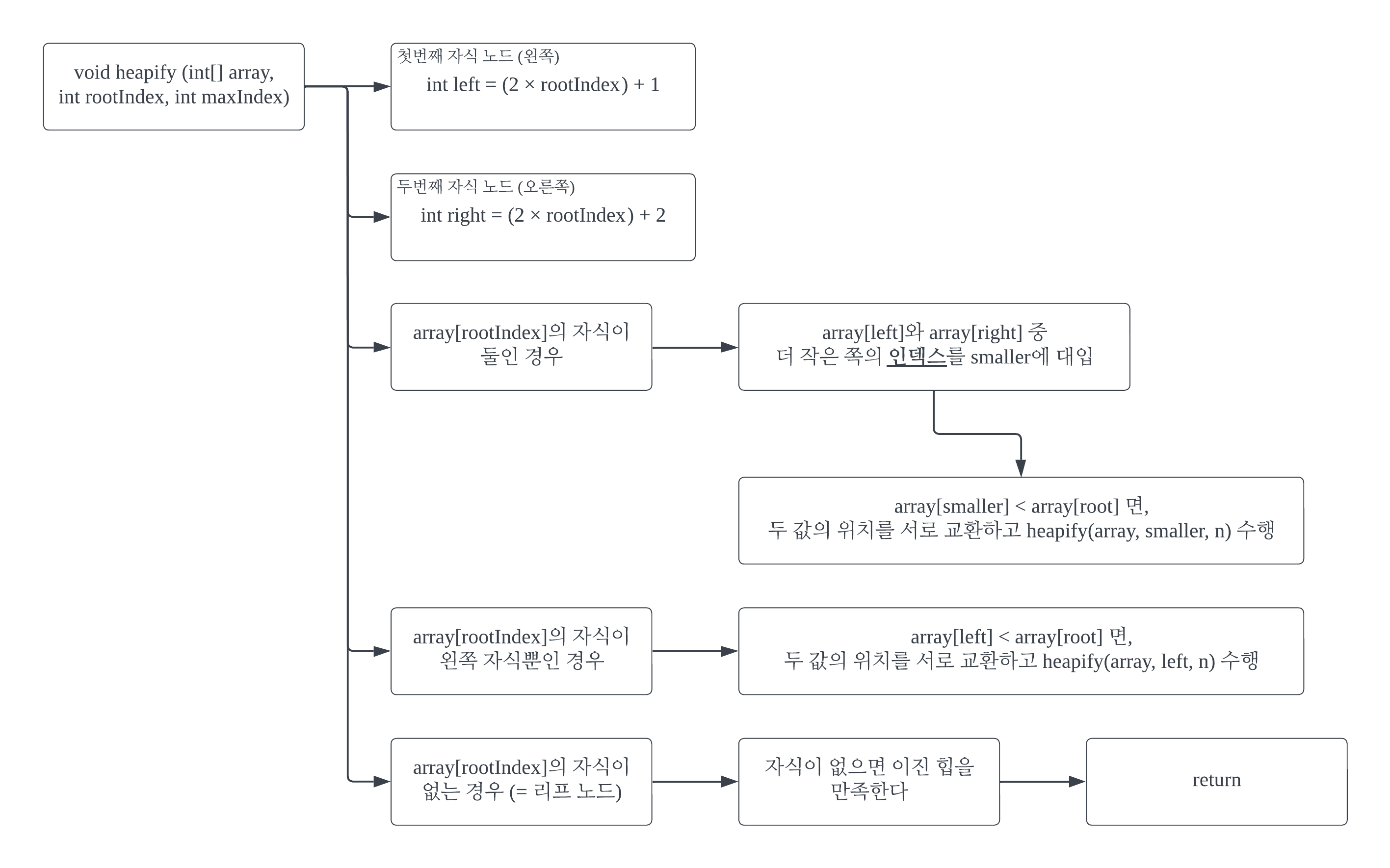
이진 힙에서 원소의 삽입 또는 삭제가 발생하면, 최소 힙 또는 최대 힙이 아닌 단순한 완전 이진 트리가 될 수 있다. heapify()는 이 완전 이진 트리가 다시 이진 힙이 되도록 수선하는 작업을 한다. heapify()는 매달린 두 서브 노드 (2개의 자식 노드)가 이진 힙을 만족한다는 전제 하에 사용하는 함수다. 따라서, 루트 노드 외에 다른 노드가 이진 힙을 만족하지 않는다면, heapify()를 사용해도 이진 힙을 만족하는 array를 보장할 수 없다. 반면, buildHeap()는 heapify()를 응용한 함수라서 어떤 array를 매개변수로 넣든 이진 힙으로 수선해서 반환한다.
#1-7
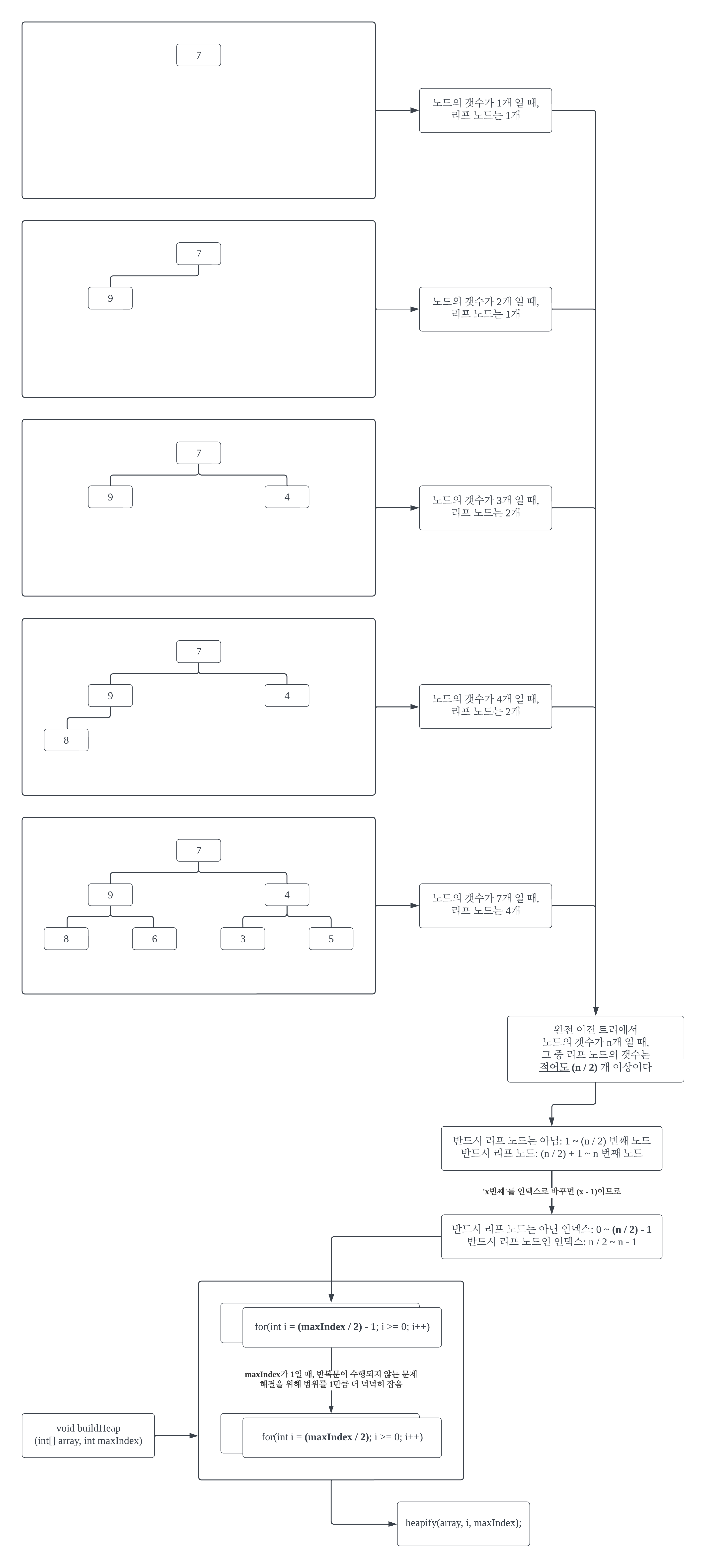
heapify()는 매달린 두 서브 노드 (2개의 자식 노드)가 이진 힙을 만족한다는 전제 하에 사용하는 함수라고 했는데, 리프 노드는 그 자체로 이진 힙을 만족한다. 리프 노드에서부터 시작해서 루트 노드까지 올라가며 heapify()를 수행하면, 중구난방인 배열을 이진 힙을 만족하는 배열로 탈바꿈 시킬 수 있다. 반드시 리프 노드인 영역은 피해서 heapify()를 수행한다. 이는 알고리즘 수행 시간의 낭비를 줄이기 위함으로, 리프 노드를 heapify() 해봤자 리프 노드 처음 그대로를 뱉어내기 때문이다.
#1-8
힙 정렬 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 힙 정렬(Heap sort)이란 최대 힙 트리나 최소 힙 트리를 구성해 정렬을 하는 방법으로서, 내림차순 정렬을 위해서는 최소 힙을 구성하고 오름차순 정렬을 위해서
ko.wikipedia.org
힙 정렬의 총 비교 횟수 계산은 해당 링크로 대체한다.
#2 코드
#2-1 자바
public static void HeapSort(int[] array, int startIndex, int endIndex) {
int[] slicedArray = new int[endIndex - startIndex + 1];
for(int i = 0; i < slicedArray.length; i++) {
slicedArray[i] = array[startIndex + i];
}
buildHeap(slicedArray);
for(int maxIndex = (slicedArray.length - 1); maxIndex >= 1; maxIndex--) {
int temp = slicedArray[0];
slicedArray[0] = slicedArray[maxIndex];
slicedArray[maxIndex] = temp;
// maxIndex는 트리에서 제거된 취급이다. 따라서, maxIndex - 1까지 수선한다.
heapify(slicedArray, 0, maxIndex - 1);
}
int[] reversedArray = new int[slicedArray.length];
for(int i = 0; i < reversedArray.length; i++) {
reversedArray[i] = slicedArray[slicedArray.length - 1 - i];
}
for(int i = 0; i < reversedArray.length; i++) {
array[startIndex + i] = reversedArray[i];
}
}
private static void heapify(int[] array, int rootIndex, int maxIndex) {
int left = (rootIndex * 2) + 1;
int right = (rootIndex * 2) + 2;
int smaller = -1;
// array[rootIndex]의 자식이 둘인 경우
if(right <= maxIndex) {
if(array[left] < array[right]) {
smaller = left;
} else {
smaller = right;
}
// array[rootIndex]의 자식이 왼쪽 하나인 경우
} else if(left <= maxIndex){
smaller = left;
// array[rootIndex]의 자식이 없는 경우 (= 리프 노드)
} else {
return;
}
// 최소 힙이므로 array[rootIndex]가 더 작아야 한다
if(array[smaller] < array[rootIndex]) {
// 두 값의 위치 교환
int temp = array[smaller];
array[smaller] = array[rootIndex];
array[rootIndex] = temp;
// smaller를 rootIndex로 하는 heapify() 재귀적 수행
heapify(array, smaller, maxIndex);
}
}
// 알고리즘에서 직관적인 이해를 위해 매개 변수에 넣었던 maxIndex를 함수 내부로 이동시켰다.
private static void buildHeap(int[] array) {
int maxIndex = array.length - 1;
for(int i = (maxIndex / 2); i >= 0; i--) {
heapify(array, i, maxIndex);
}
}
#2-2 코틀린
fun heapSort(array : Array<Int>, startIndex : Int, endIndex : Int) {
val slicedArray = array.sliceArray(startIndex..endIndex)
buildHeap(slicedArray)
for(maxIndex : Int in (slicedArray.size - 1) downTo 1) {
val temp = slicedArray[0]
slicedArray[0] = slicedArray[maxIndex]
slicedArray[maxIndex] = temp
// maxIndex는 트리에서 제거된 취급이다. 따라서, maxIndex - 1까지 수선한다.
heapify(slicedArray, 0, maxIndex - 1)
}
slicedArray.reverse()
for(i : Int in 0..(slicedArray.size - 1)) {
array[startIndex + i] = slicedArray[i]
}
}
fun heapify(array: Array<Int>, rootIndex: Int, maxIndex: Int) {
val left = (rootIndex * 2) + 1
val right = (rootIndex * 2) + 2
var smaller = -1
// array[rootIndex]의 자식이 둘인 경우
if(right <= maxIndex) {
if(array[left] < array[right]) {
smaller = left
} else {
smaller = right
}
// array[rootIndex]의 자식이 왼쪽 하나인 경우
} else if(left <= maxIndex) {
smaller = left
// array[rootIndex]의 자식이 없는 경우 (= 리프 노드)
} else {
return
}
// 최소 힙이므로 array[rootIndex]가 더 작아야 한다
if(array[smaller] < array[rootIndex]) {
// 두 값의 위치 교환
val temp = array[smaller]
array[smaller] = array[rootIndex]
array[rootIndex] = temp
// smaller를 rootIndex로 하는 heapify() 재귀적 수행
heapify(array, smaller, maxIndex)
}
}
// 알고리즘에서 직관적인 이해를 위해 매개 변수에 넣었던 maxIndex를 함수 내부로 이동시켰다.
fun buildHeap(array : Array<Int>) {
val maxIndex = array.size - 1
for(i : Int in (maxIndex / 2) downTo 0) {
heapify(array, i, maxIndex)
}
}
#3 요약
힙 정렬은, 이진 '힙'의 루트 노드가 항상 최솟값 또는 최댓값을 가진다는 것을 이용하는 일종의 선택 정렬이다.
#4 이 개념이 사용된 글
11650 - 좌표 정렬하기
#1 알고리즘 힙 정렬 (Heap Sort) #1 알고리즘 힙(heap)이라는 영어 단어의 사전적 의미는 쌓아 놓은 무더기다. 그리고 이 단어는 프로그래밍에서도 사용된다. 첫째로 메모리 영역에서, 둘째로 자료구
kenel.tistory.com
'깨알 개념 📑 > 알고리즘' 카테고리의 다른 글
| 정렬 - 퀵 정렬 (Quick Sort) (0) | 2023.12.01 |
|---|---|
| 정렬 - 삽입 정렬 (Insertion Sort) (0) | 2023.11.29 |
| 정렬 - 병합 정렬 (Merge Sort) (1) | 2023.11.14 |
| 정렬 - 버블 정렬 (Bubble Sort) (0) | 2023.11.13 |
| 중복된 원소 값이 있는 경우의 이진 탐색 (Binary Search) (0) | 2023.11.07 |