#1 알고리즘
#1-1
이진 탐색 (Binary search)
#1 알고리즘 이렇게 해서 x의 인덱스 i를 찾으면 좋겠지만, 이 x가 배열 values 어디에도 존재하지 않는 경우도 있을 것이다. 이 경우엔 어떻게 처리해야 할까? 업 앤 다운 게임은 우리나라에선 소주
kenel.tistory.com
해당 글에서 이어진다.
#1-2
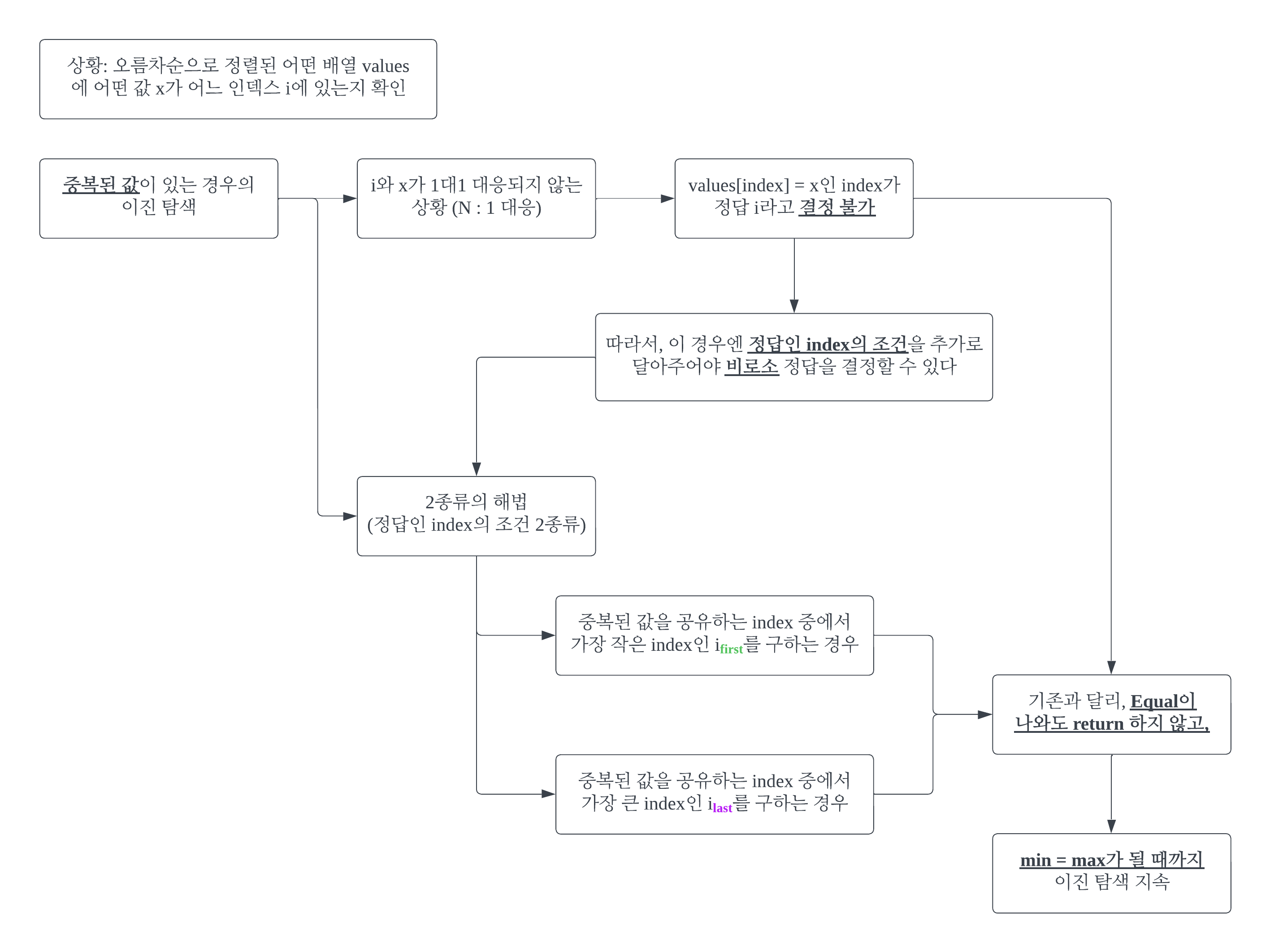
#1-3
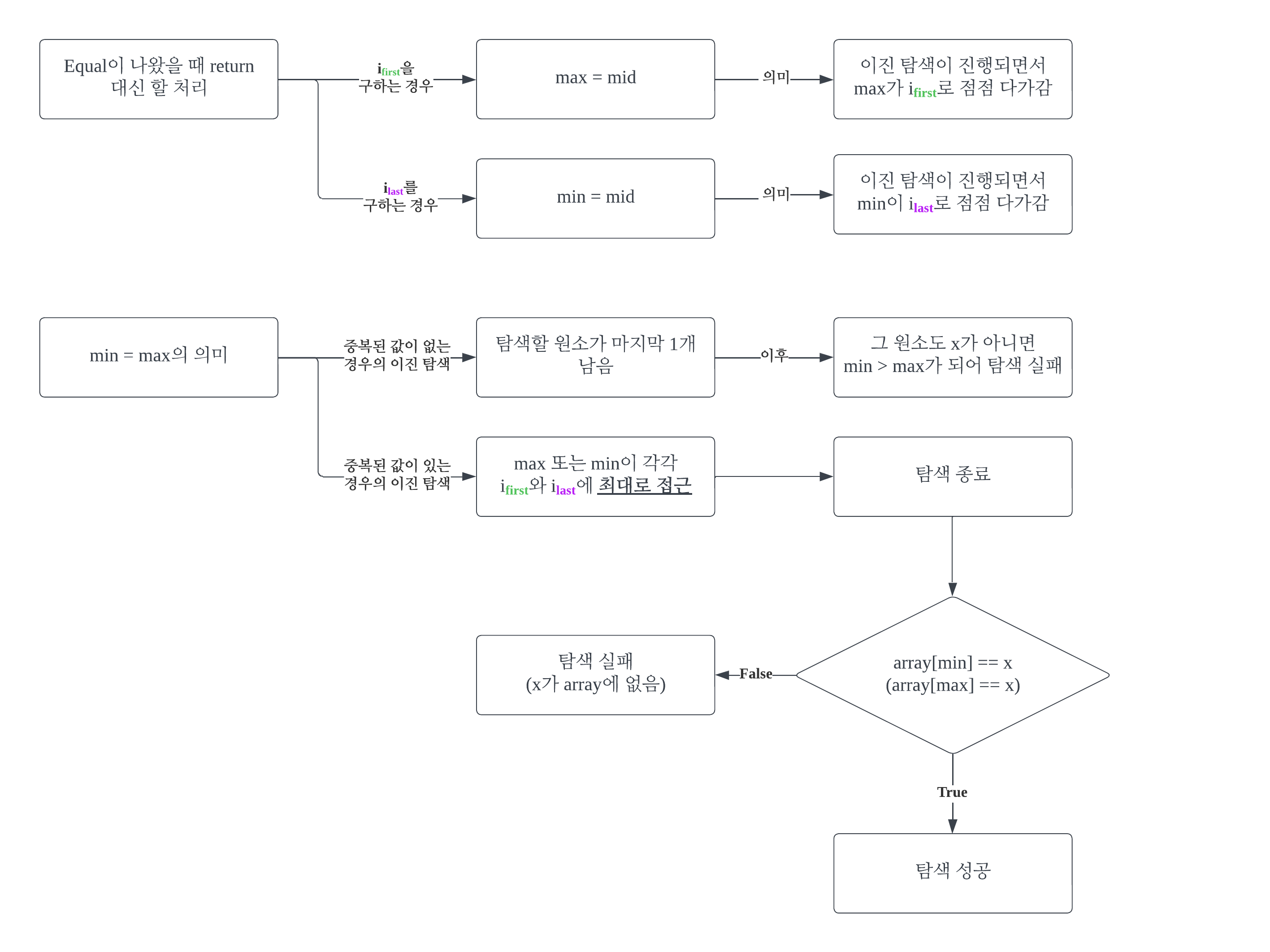
중복된 값이 없는 경우의 이진 탐색에선 min < max가 되는 시점이 while의 탈출 시점이었다. 반면, 중복된 값이 있는 경우의 이진 탐색에선 min = max가 되는 시점이 while의 탈출 시점이다. min = max는 검색 범위가 i에 최대로 접근 즉, 아예 같은 값이 되었다는 의미다.
#1-4

binarySearch() 대비 binarySearchFirstIndex() 또는 binarySearchLastIndex()에서 다른 부분을 빨갛게 강조 표시했다. 하지만, 납득이 되지 않는 부분이 보인다. 바로 binarySearchLastIndex()에서 mid = (min + max) / 2에 그치지 않고 추가로 1을 더한 부분이다. 게다가 binarySearchFirstIndex()는 mid를 정의하는 부분이 binarySearch()와 똑같은데 binarySearchLastIndex() 혼자만 다른 것은 더더욱 의아하다.
#1-5
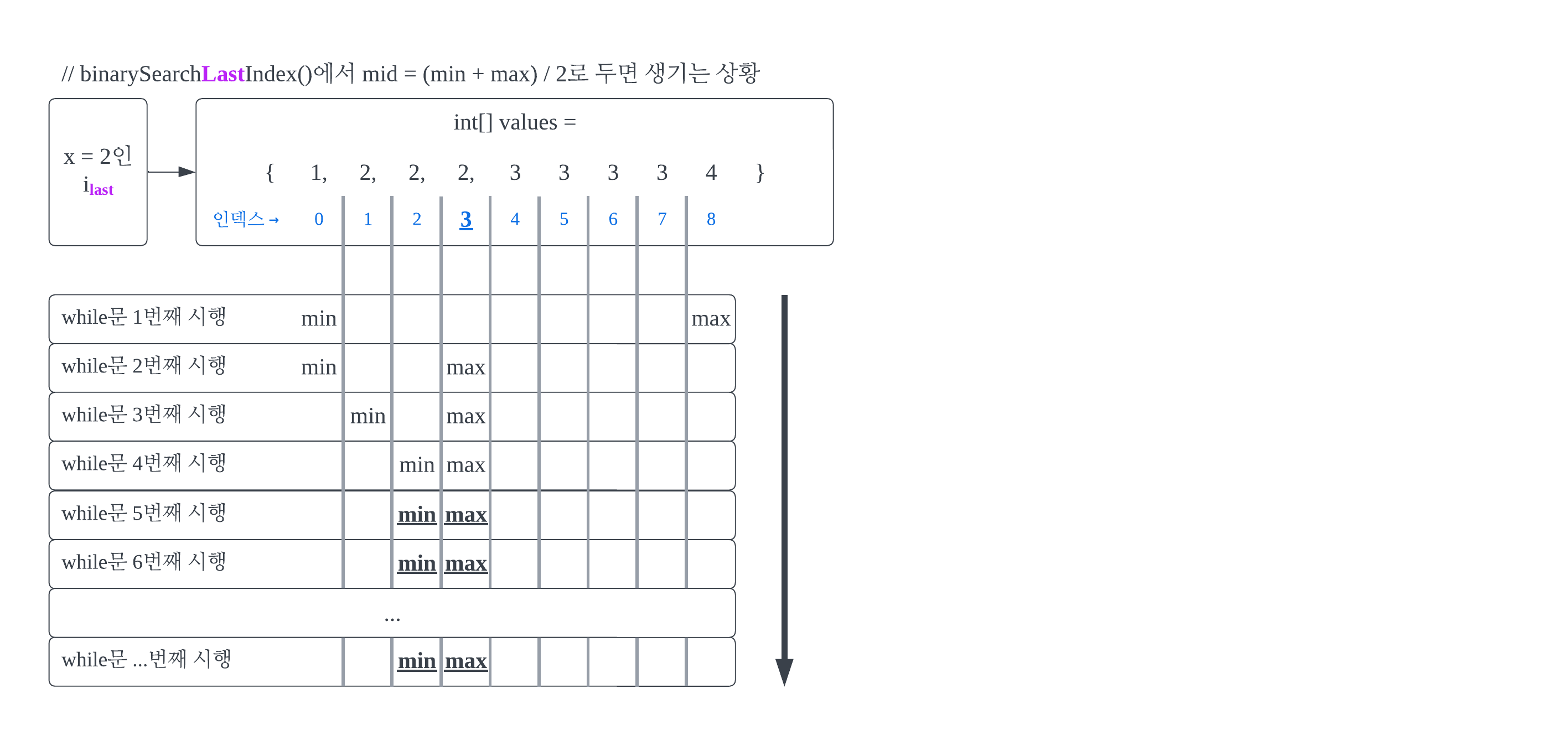
binarySearchLastIndex()의 mid에 추가로 1을 더하지 않았다면 발생하는 상황이다. min과 max가 영원히 같지 않기 때문에 프로그램이 binarySearchLastIndex()의 return을 무한히 기다리게 된다. 이 상황은 int형끼리의 / 연산의 특징에서 기인한다.
#1-6

#1-7

알고리즘을 이렇게 간소화 할 수도 있다. while문이 진행됨에 따라, binarySearchFirstIndex()의 max 또는 binarySearchLastIndex()의 min이 각각 ifirst와 ilast에 같아질 때까지 접근하는 경향성이 간소화 전과 동일하게 유지되기 때문이다. 물론 알고리즘의 성능(계산 속력)은 미세먼지만큼이라도 떨어질 것이다.
#2 코드
#2-1 자바
public static int binarySearchFirstIndex(int[] values, int x) {
int min = 0;
int max = values.length - 1;
while (min < max) {
int mid = (min + max) / 2;
// up
if (values[mid] < x) {
min = mid + 1;
// equal
} else if (values[mid] == x) {
max = mid;
// down
} else { // values[mid] > x
max = mid - 1;
}
}
if(values[min] == x) {
return min;
} else {
return -1;
}
}
public static int binarySearchLastIndex(int[] values, int x) {
int min = 0;
int max = values.length - 1;
while (min < max) {
int mid = (min + max) / 2;
// up
if (values[mid] < x) {
min = mid + 1;
// equal
} else if (values[mid] == x) {
min = mid;
// down
} else { // values[mid] > x
max = mid - 1;
}
}
if(values[max] == x) {
return max;
} else {
return -1;
}
}
#2-2 코틀린
fun binarySearchFirstIndex(values : Array<Int>, x : Int) : Int {
var min = 0
var max = values.size - 1
while(min < max) {
val mid = (min + max) / 2
// up
if(values[mid] < x) {
min = mid + 1
// equal
} else if(values[mid] == x) {
max = mid
// down
} else { // values[mid] > x
max = mid - 1
}
}
if(values[min] == x) {
return min
} else {
return -1
}
}
fun binarySearchLastIndex(values : Array<Int>, x : Int) : Int {
var min = 0
var max = values.size - 1
while(min < max) {
val mid = (min + max) / 2 + 1
// up
if(values[mid] < x) {
min = mid + 1
// equal
} else if(values[mid] == x) {
min = mid
// down
} else { // values[mid] > x
max = mid - 1
}
}
if(values[max] == x) {
return max
} else {
return -1
}
}
#3 요약
중복된 원소 값이 있는 경우의 이진 탐색은, 같은 값을 공유하는 인덱스들 중에서 첫번째 인덱스 또는 마지막 인덱스에 점진적으로 접근한다.
#4 이 개념이 사용된 글
[백준] 1654 (랜선 자르기)
#1 알고리즘 #1-1 #1-2 중복된 원소 값이 있는 경우의 이진 탐색 (Binary Search) #1 알고리즘 이진 탐색 (Binary search) #1 알고리즘 이렇게 해서 x의 인덱스 i를 찾으면 좋겠지만, 이 x가 배열 values 어디에도
kenel.tistory.com
[백준] 2805 (나무 자르기)
#1 개요#1-1 문제 이해'나무를 자르는 높이(cuttingHeight)'가 무엇인지를 묻는 문제다. 그리고 cuttingHeight의 범위는 0 ~ 1,000,000,000이다. 따라서, cuttingHeight를 1씩 증가시켜서 일일히 확인하는 방법은 시
kenel.tistory.com
'깨알 개념 📑 > 알고리즘' 카테고리의 다른 글
| 정렬 - 병합 정렬 (Merge Sort) (2) | 2023.11.14 |
|---|---|
| 정렬 - 버블 정렬 (Bubble Sort) (0) | 2023.11.13 |
| 이진 탐색 (Binary search) (0) | 2023.11.06 |
| 정렬 - 선택 정렬 (Selection Sort) (0) | 2023.11.02 |
| 배열의 길이(length)와 원소의 순번(index) (0) | 2023.11.01 |