#1 알고리즘
#1-1
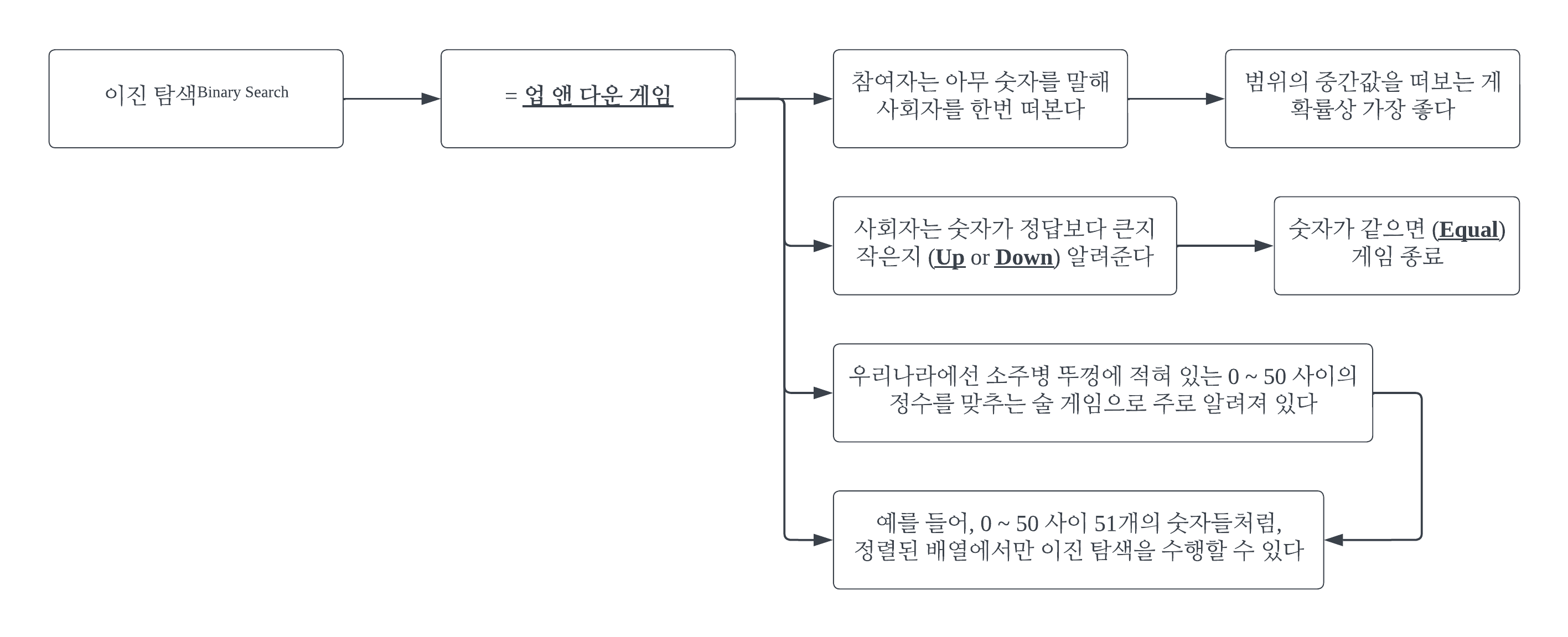
#1-2
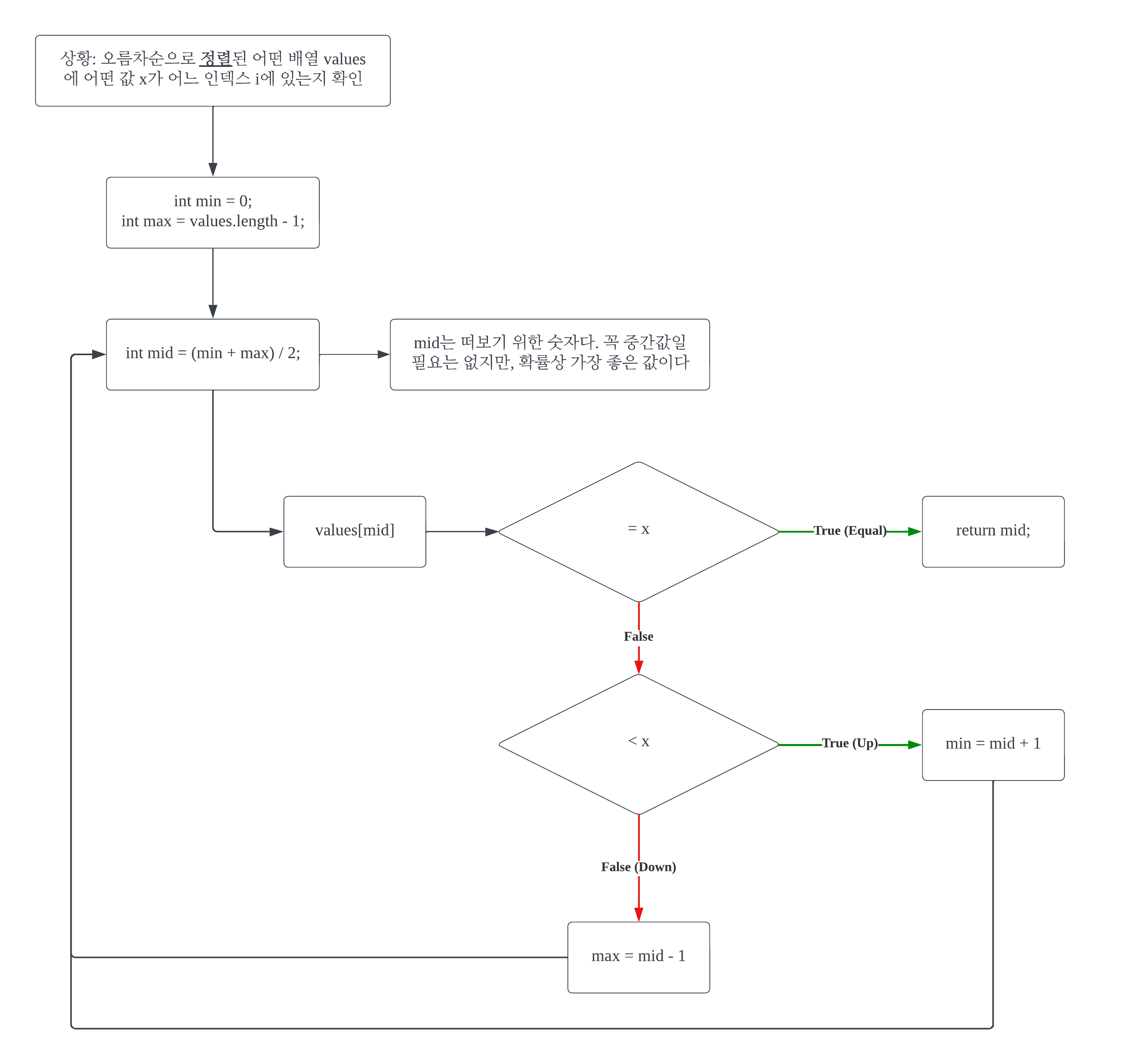
이렇게 해서 x의 인덱스 i를 찾으면 좋겠지만, 이 x가 배열 values 어디에도 존재하지 않는 경우도 있을 것이다. 이 경우엔 어떻게 처리해야 할까?
#1-3
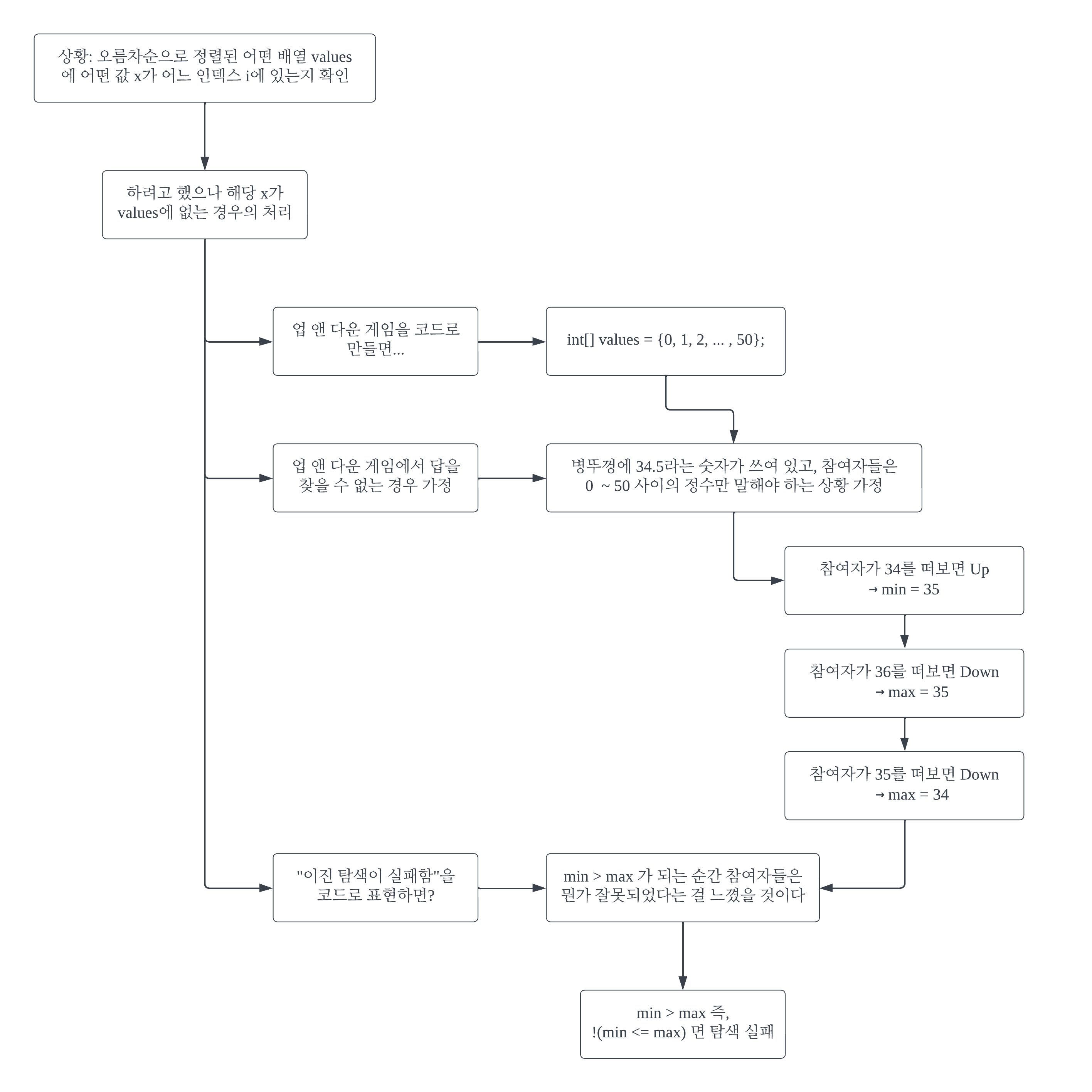
업 앤 다운 게임은 우리나라에선 소주병 뚜껑에 적혀 있는 0 ~ 50 사이의 정수를 가지고 맞추는 술 게임의 이미지가 강하다. 어떤 상황을 가정해보겠다. 어느 병뚜껑엔 알 수 없는 이유로 34.5라는 정수가 아닌 수가 적혀 있었다. 사회자는 병뚜껑에 쓰인 숫자를 보고 당황했지만, 장난기가 발동해 그냥 게임을 진행해 보기로 했다. 참여자들은 병뚜껑에 쓰인 숫자가 정수가 아닐 거라고는 생각지 못하고 업 앤 다운 게임에 임할 것이다. 이 업 앤 다운 게임은 실패할 운명이다. 하지만, 이 사례를 상상해 보면서 이진 탐색이 실패했음을 어떻게 판단할 것인가를 도출해 낼 수 있다.
#1-4

Up이라고 판단하는 기준인 value[mid] < x의 의미는 x값의 인덱스 i가 mid보다 크다(Up)는 의미다. i는 binarySearch()에서 반환(return)할 값이다.
#1-5
중복된 원소 값이 있는 경우의 이진 탐색 (Binary Search)
#1 알고리즘 이진 탐색 (Binary search) #1 알고리즘 이렇게 해서 x의 인덱스 i를 찾으면 좋겠지만, 이 x가 배열 values 어디에도 존재하지 않는 경우도 있을 것이다. 이 경우엔 어떻게 처리해야 할까? 업
kenel.tistory.com
values에 중복되는 원소가 있는 경우의 알고리즘
#2 코드
#2-1 자바
private static int binarySearch(int[] values, int x) {
int min = 0;
int max = values.length - 1;
while (min <= max) {
int mid = (min + max) / 2; // int끼리 나누면 소수점 아래는 버려진다. (반올림 아님)
// up
if (values[mid] < x) {
min = mid + 1;
// equal
} else if (values[mid] == x) {
return mid;
// down
} else { // values[mid] > x
max = mid - 1;
}
}
return -1;
}
#2-2 코틀린
fun binarySearch(values : Array<Int>, x : Int) : Int {
var min = 0
var max = values.size - 1
while(min <= max) {
val mid = (min + max) / 2
// up
if(values[mid] < x) {
min = mid + 1
// equal
} else if(values[mid] == x) {
return mid
// down
} else { // values[mid] > x
max = mid - 1
}
}
return -1
}
#3 요약
이진 탐색은 업 앤 다운 게임이다.
'깨알 개념 📑 > 알고리즘' 카테고리의 다른 글
| 정렬 - 병합 정렬 (Merge Sort) (2) | 2023.11.14 |
|---|---|
| 정렬 - 버블 정렬 (Bubble Sort) (0) | 2023.11.13 |
| 중복된 원소 값이 있는 경우의 이진 탐색 (Binary Search) (0) | 2023.11.07 |
| 정렬 - 선택 정렬 (Selection Sort) (0) | 2023.11.02 |
| 배열의 길이(length)와 원소의 순번(index) (0) | 2023.11.01 |