#1 알고리즘
#1-1

#1-2

#1-3

#1-4
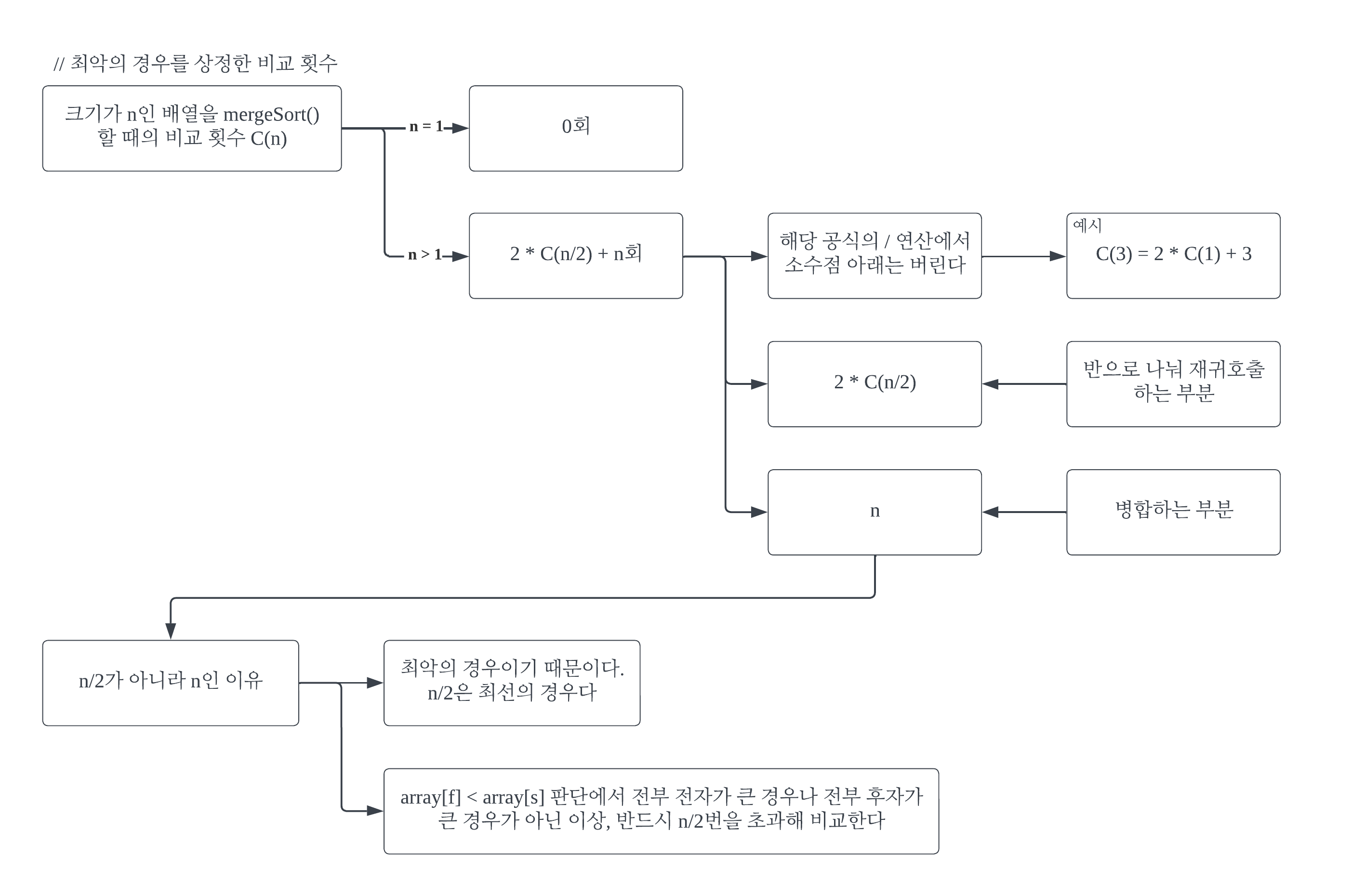
#1-5

병합 정렬의 총 비교 횟수는, 최악의 경우 nlog2n이다
#2 코드
#2-1 자바
public static void mergeSort(int[] array, int startIndex, int endIndex) {
// (startIndex < endIndex)의 의미: 배열의 크기가 2이상이다.
if(startIndex < endIndex) {
int midIndex = (startIndex + endIndex) / 2;
mergeSort(array, startIndex, midIndex);
mergeSort(array, (midIndex + 1), endIndex);
merge(array, startIndex, midIndex, endIndex);
}
}
private static void merge(int[] array, int startIndex, int midIndex, int endIndex) {
// array에서 나뉜 'f'irst 부분을 순회할 인덱스 f
int f = startIndex; // f의 최댓값은 midIndex
// array에서 나뉜 's'econd 부분을 순회할 인덱스 s
int s = midIndex + 1; // s의 최댓값은 endIndex
// 'T'emporary 배열 그리고 이 배열을 순회할 인덱스 t
int[] T = new int[endIndex - startIndex + 1];
int t = 0;
while(f <= midIndex && s <= endIndex) {
if(array[f] < array[s]) {
T[t++] = array[f++];
} else {
T[t++] = array[s++];
}
}
// f의 영역이 남았다면 비워준다
while(f <= midIndex) {
T[t++] = array[f++];
}
// s의 영역이 남았다면 비워준다
while(s <= endIndex) {
T[t++] = array[s++];
}
for(int i = 0; i < T.length; i++) {
array[startIndex + i] = T[i];
}
}
#2-2 코틀린
fun mergeSort(array: Array<Int>, startIndex : Int, endIndex : Int) {
// (startIndex < endIndex)의 의미: 배열의 크기가 2이상이다.
if(startIndex < endIndex) {
val midIndex = (startIndex + endIndex) / 2
mergeSort(array, startIndex, midIndex)
mergeSort(array, (midIndex + 1), endIndex)
merge(array, startIndex, midIndex, endIndex)
}
}
fun merge(array : Array<Int>, startIndex: Int, midIndex : Int, endIndex: Int) {
// array에서 나뉜 'f'irst 부분을 순회할 인덱스 f
var f = startIndex // f의 최댓값은 midIndex
// array에서 나뉜 's'econd 부분을 순회할 인덱스 s
var s = midIndex + 1 // s의 최댓값은 endIndex
// 'T'emporary 배열 그리고 이 배열을 순회할 인덱스 t
val T : Array<Int> = Array(endIndex - startIndex + 1) { 0 }
var t = 0
while(f <= midIndex && s <= endIndex) {
if(array[f] < array[s]) {
T[t++] = array[f++]
} else {
T[t++] = array[s++]
}
}
// f의 영역이 남았다면 비워준다
while(f <= midIndex) {
T[t++] = array[f++]
}
// s의 영역이 남았다면 비워준다
while(s <= endIndex) {
T[t++] = array[s++]
}
for(i : Int in 0..(T.size - 1)) {
array[startIndex + i] = T[i]
}
}
#3 요약
병합 정렬은 문제를 2개로 나눈 후 '병합'하는 정렬이다
#4 이 개념이 사용된 글
2751
#1 알고리즘 병합 정렬 (Merge Sort) #1 알고리즘 병합 정렬의 총 비교 횟수는, 최악의 경우 nlog2n이다 #2 코드 (자바) public static void mergeSort(int[] array, int startIndex, int endIndex) { // (startIndex < endIndex)의 의
kenel.tistory.com
11651 - 좌표 정렬하기 2
#1 알고리즘 11650 - 좌표 정렬하기 #1 알고리즘 힙 정렬 (Heap Sort) #1 알고리즘 힙(heap)이라는 영어 단어의 사전적 의미는 쌓아 놓은 무더기다. 그리고 이 단어는 프로그래밍에서도 사용된다. 첫째로
kenel.tistory.com
[백준] 11399 - ATM
#1 알고리즘 병합 정렬 (Merge Sort) #1 알고리즘 병합 정렬의 총 비교 횟수는, 최악의 경우 nlog2n이다 #2 코드 (자바) public static void mergeSort(int[] array, int startIndex, int endIndex) { // (startIndex < endIndex)의 의
kenel.tistory.com
'깨알 개념 📑 > 알고리즘' 카테고리의 다른 글
| 정렬 - 삽입 정렬 (Insertion Sort) (0) | 2023.11.29 |
|---|---|
| 정렬 - 힙 정렬 (Heap Sort) (0) | 2023.11.20 |
| 정렬 - 버블 정렬 (Bubble Sort) (0) | 2023.11.13 |
| 중복된 원소 값이 있는 경우의 이진 탐색 (Binary Search) (0) | 2023.11.07 |
| 이진 탐색 (Binary search) (0) | 2023.11.06 |