#1 알고리즘
#1-1 정의

동적 프로그래밍을 한 줄 요약하면 중복의 제거다. 정적(static)이라는 개념과 반대되는 개념으로서, 동적(dynamic)이라는 단어가 이름에 붙었다. 확실히 static이 붙을 만한 작업은 아니지만, 그렇다고 많은 단어들 중에 굳이 dynamic가 붙을 필요 또한 없다. '동적', ' dynamic'이라는 이름은 동적 프로그래밍의 (중복의 제거라는) 핵심을 직관적으로 이해하지 못하게 만든다. 하지만, 관례적으로 이미 굳어진 이름이라 앞으로도 쓰일 것이라는 사실은 안타까우면서도 분명하다.
#1-2 종류
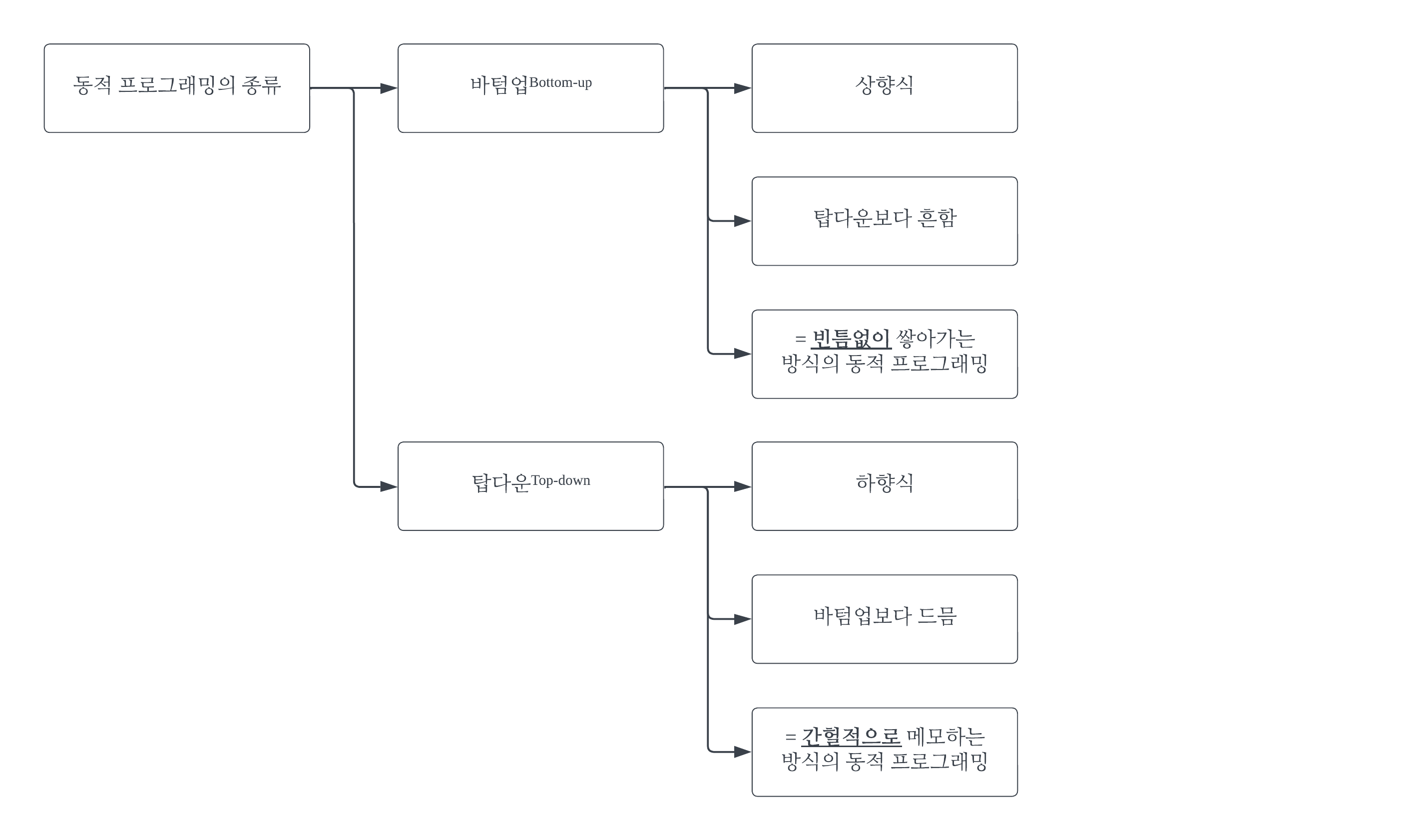
동적 프로그래밍은 이와 같이 2가지 방식으로 나뉜다.
#1-3 상향식(Bottom-up) 접근
[백준] 17626 - Four Squares
#1 알고리즘 123 123 재귀 함수가 평균적으로 1만 번 언저리 호출되었을 때 즈음 스택오버플로우가 걸렸다. #2 여담 dp문제인줄 모르고 하루 종일을 날렸다. 그리고 dp문제 특징이 죄다 캐싱용 변수
kenel.tistory.com
상향식 동적 프로그래밍의 풀이의 예는 위 게시글에 있다. 해당 게시글의 #1-4과 #3을 보면 된다. 코드를 보면, 상향식 접근을 '빈틈없이 쌓아가는 방식'이라고 한 이유를 알 수 있다. 해당 게시글의 배열 dp는 인덱스 0을 제외하곤 전부 다 초깃값이 아닌 값이 할당되어 있다. 틈이 없다. 앞으로 지금보다 더 큰 문제를 푸는 데에 있어, 어떤 작은 문제가 쓰일 지 아닐 지는 우리가 폰 노이만이 아닌 이상 모르기 때문이다. 따라서 빈틈없이 모든 문제의 해를 구해두는 것이다. 여기에서 상향식 접근의 단점을 알 수 있다. 바로 메모리를 많이 차지한다는 점이다.
여담으로, 해당 게시글의 #4를 보면 하향식 동적 프로그래밍의 단점도 알 수 있다. 재귀호출이 과도하게 많아지면 스택 오버플로우 런타임 에러가 발생한다. 따라서 과도하게 많은 재귀호출이 발생하는 문제라면 하향식 동적 프로그래밍은 쓰기 어렵다.
#1-4 하향식(Top-down) 접근
[백준] 1003 - 피보나치 함수
#1 알고리즘 #2 코드 (자바) import java.util.*; public class Main { public static Map map = new HashMap(); public static void main(String[] args) { Integer[] seedData0 = {1, 0}; Integer[] seedData1 = {0, 1}; map.put(0, seedData0); map.put(1, seedDat
kenel.tistory.com
이번에는 하향식 동적 프로그래밍의 예다. 해당 게시글의 fibonacci()는 큰 문제를 작은 문제로 쪼개나간다. 이때, 한 번 값이 구해진 문제는 Map 객체에 말 그대로 '메모'되어, 다음에 같은 문제를 만나면 다시 계산할 필요없이 메모했던 걸 그대로 가져다가 쓴다. 큰 문제를 쪼개어 나온 어떤 작은 문제는 반드시 그 해를 구해야 하는 필수 목표가 되며, 해를 구한 김에 메모까지 하여 미래에 혹시라도 나올 같은 문제에 대비하는 것이다.
#1-5 두 접근법의 비교
상향식 접근과는 달리, 하향식 접근의 코드에선 어떤 작은 문제의 해가 '메모'되었는지 체크하는 부분이 있다. 상향식 접근에서는 작은 문제를 단 하나도 빠뜨리지 않고 마치 깜지하듯 풀어가며 위로 올라가기 때문에, 작은 문제를 이전에 이미 풀어서 그 해를 제대로 저장해놓았음을 의심할 필요가 없다. 반면, 상향식 접근에서는 작은 해를 띄엄띄엄 메모하기 때문에, 어떤 작은 문제가 이전에 풀었던 것인지 확실치 않다. 따라서, 체크한다.
동적 프로그래밍의 두 종류 모두 큰 문제를 해결하기 위해서 작은 문제들의 해를 따로 저장해둔다는 점은 동일하다. 다만 그 저장의 양상이 다를 뿐이다. 상향식 접근이 '빈틈없이 쌓아간다'라면, 하향식 접근은 이른바 '빈틈있게 쌓아간다'고 말할 수 있다. 또, 하향식 접근이 메모라면, 상향식 접근은 깜지다. 그리고 하향식 접근에서의 메모를 특별히, 캐싱 또는 메모이제이션이라고 부른다 (상향식 접근에서의 메모(깜지)도 마찬가지로 캐싱이라고 부르는 것으로 보인다. 엄밀히 구분되지는 않나보다).
#1-6 캐싱

메모이제이션(Memoization, 메모)은 메모리제이션(Memorization, 기억)과 다른 단어다. 메모이제이션은 메모(Memo)에서 파생된 단어다. 메모이제이션은 약간 학술적인 늬앙스의 단어며, 실무에서는 주로 캐싱이라는 말로 불린다고 한다. 캐싱이 동적 프로그래밍에 포함되는 개념은 아니다. 즉, 동적 프로그래밍의 목적으로만 한정되어 쓰이는 개념이 아니다. 말 그대로 '메모하기'인데 얼마나 추상적이며, 그렇기에 얼마나 큰 활용 가능성을 지녔겠는가?
#2 동적 프로그래밍 사용 시의 마음가짐
[백준] 11053 (가장 긴 증가하는 부분 수열)
#1 알고리즘 Longest increasing subsequence - WikipediaFrom Wikipedia, the free encyclopedia Computer science problem In computer science, the longest increasing subsequence problem aims to find a subsequence of a given sequence in which the subsequenc
kenel.tistory.com
동적 프로그래밍은 도구일 뿐이다. 결국 사용자는 사람이다.
#3 요약
동적 프로그래밍은 중복 제거다.
#4 이 개념이 사용된 글
#4-1 상향식(Bottom-up) 접근
[백준] 17626 - Four Squares
#1 알고리즘 123 123 재귀 함수가 평균적으로 1만 번 언저리 호출되었을 때 즈음 스택오버플로우가 걸렸다. #2 여담 dp문제인줄 모르고 하루 종일을 날렸다. 그리고 dp문제 특징이 죄다 캐싱용 변수
kenel.tistory.com
[백준] 9095 - 1, 2, 3 더하기
#1 알고리즘 #1-1 동적 프로그래밍 (Dynamic Programming), 상향식(Bottom-up) 및 하향식(Top-down) 접근 #1 알고리즘 동적 프로그래밍을 한 줄 요약하면 중복의 제거다. 정적(static)이라는 개념과 반대되는 개념
kenel.tistory.com
[백준] 1676 (팩토리얼 0의 개수)
#1 알고리즘 #1-1 문제의 핵심 이 문제의 핵심은, x!가 가지고 있는 2*5 쌍의 갯수만큼 뒤에 0이 붙는다는 규칙의 파악이다. #1-2 상향식 동적 프로그래밍 동적 프로그래밍 (Dynamic Programming), 상향식(Bot
kenel.tistory.com
#4-2 하향식(Top-down) 접근
[백준] 1003 - 피보나치 함수
#1 알고리즘 #2 코드 (자바) import java.util.*; public class Main { public static Map map = new HashMap(); public static void main(String[] args) { Integer[] seedData0 = {1, 0}; Integer[] seedData1 = {0, 1}; map.put(0, seedData0); map.put(1, seedDat
kenel.tistory.com
[백준] 1463 (1로 만들기)
#1 알고리즘 동적 프로그래밍 (Dynamic Programming), 상향식(Bottom-up) 및 하향식(Top-down) 접근 #1 알고리즘 #1-1 정의 동적 프로그래밍을 한 줄 요약하면 중복의 제거다. 정적(static)이라는 개념과 반대되는
kenel.tistory.com
'깨알 개념 📑 > 알고리즘' 카테고리의 다른 글
| 그래프 - 너비 우선 탐색 (BFS, Breadth-First Search) (0) | 2024.09.23 |
|---|---|
| 그래프 - 그래프의 종류와 표현 (0) | 2024.01.09 |
| 정렬 - 퀵 정렬 (Quick Sort) (0) | 2023.12.01 |
| 정렬 - 삽입 정렬 (Insertion Sort) (0) | 2023.11.29 |
| 정렬 - 힙 정렬 (Heap Sort) (0) | 2023.11.20 |