#1 알고리즘
#1-1
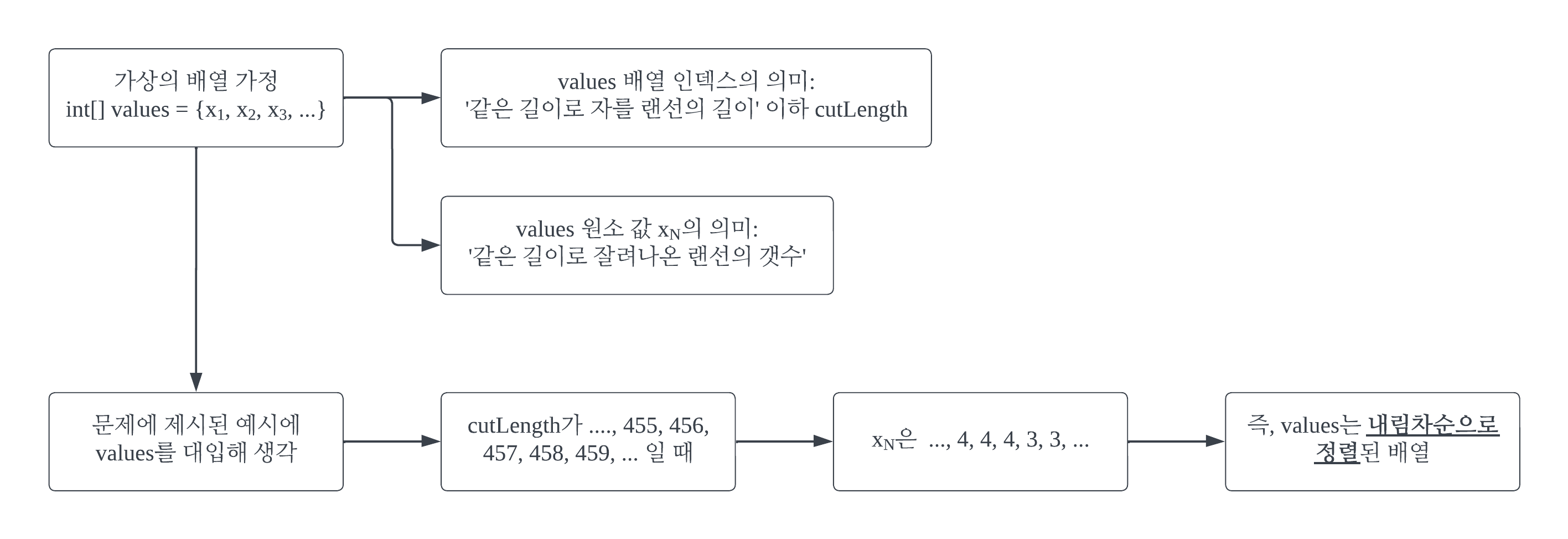
#1-2
중복된 원소 값이 있는 경우의 이진 탐색 (Binary Search)
#1 알고리즘 이진 탐색 (Binary search) #1 알고리즘 이렇게 해서 x의 인덱스 i를 찾으면 좋겠지만, 이 x가 배열 values 어디에도 존재하지 않는 경우도 있을 것이다. 이 경우엔 어떻게 처리해야 할까? 업
kenel.tistory.com
해당 글을 읽어야 이 다음 부분을 이해할 수 있다
#1-3
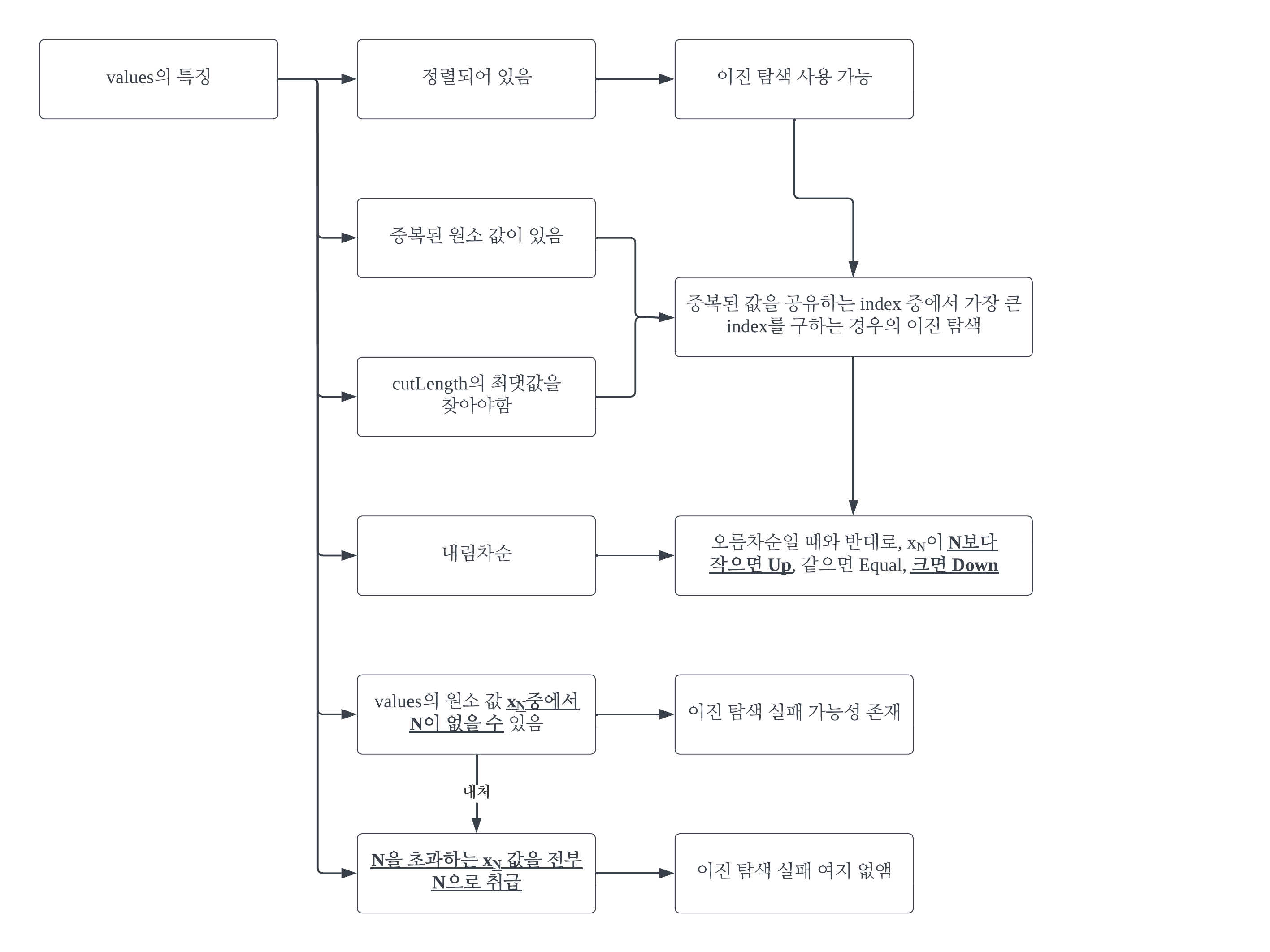
#1-4
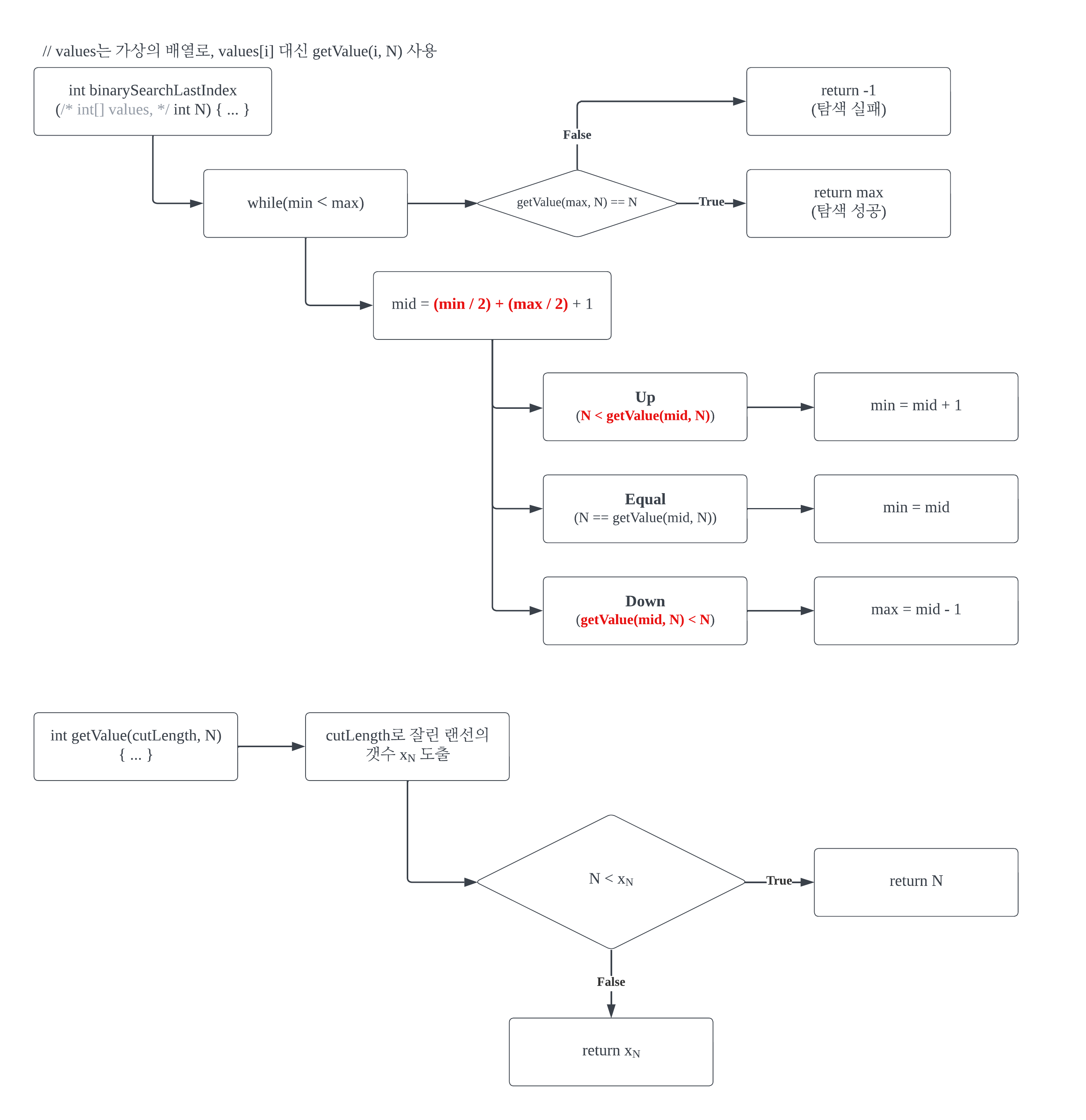
여기에서 정리했던 binarySearchLastIndex()와 다른 부분을 강조 표시했다. min과 max을 각각 2로 나눈 뒤 더하는 이유는 int형의 오버플로우 방지를 위해서다. 또, values는 내림차순이기 때문에, Up 및 Down을 판단하는 코드에서의 부등호를 반대 방향으로 돌렸다.
#2 코드
#2-1 자바
import java.util.Scanner;
public class Main {
public static int[] originalCableLengths;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int K = sc.nextInt();
int N = sc.nextInt();
sc.nextLine(); // 입력 버퍼의 첫째 줄 비워내기
originalCableLengths = new int[K];
for(int i = 0; i < originalCableLengths.length; i++) {
originalCableLengths[i] = Integer.parseInt(sc.nextLine().trim());
}
sc.close();
// values는 가상의 배열이다
int submit = binarySearchLastIndex(/* values, */ N);
System.out.println(Integer.toString(submit));
}
// 중복된 값을 공유하는 배열에서 가장 큰 index를 구하는 이진 탐색
private static int binarySearchLastIndex(/* int[] values, */ int N) {
int min = 0;
int max = (int) (Math.pow(2, 31) - 1); // (int) (Math.pow(2, 31) - 1) != (int) Math.pow(2, 31) - 1
while(min < max) {
int mid = (min / 2) + (max / 2) + 1; // 오버플로우 방지
int value = getValue(mid, N);
// up
if(N < value) { // value < N이 아닌 이유는, 배열 values가 내림차순으로 정렬되어 있기 때문이다.
min = mid + 1;
// equal
} else if(N == value) {
min = mid;
// down
} else { // N < value
max = mid - 1;
}
}
if(getValue(max, N) == N) {
return max;
} else {
return -1;
}
}
// values[cutLength]와 같은 값을 반환함.
private static int getValue(int cutLength, int N) {
int cutCableCount = 0;
for(int originalCableLength : originalCableLengths) {
cutCableCount += originalCableLength / cutLength;
}
if(N < cutCableCount) {
return N;
} else {
return cutCableCount;
}
}
}
#2-2 코틀린
import kotlin.math.pow
lateinit var originalCableLengths : Array<Int>
fun main() {
val kAndN = readLine()!!.trim()
val kAndNArray = kAndN.split(" ")
val K = kAndNArray[0].toInt()
val N = kAndNArray[1].toInt()
originalCableLengths = Array(K) {0}
for(i : Int in 0..K - 1) {
originalCableLengths[i] = readLine()!!.trim().toInt()
}
// values는 가상의 배열이다
println(binarySearchLastIndex(/* values, */ N))
}
// 중복된 값을 공유하는 배열에서 가장 큰 index를 구하는 이진 탐색
fun binarySearchLastIndex(/* values : Array<Int>, */ N: Int): Int {
var min = 0;
var max = (2.0.pow(31.0) - 1).toInt() // (2.0.pow(31.0) - 1).toInt() != 2.0.pow(31.0).toInt() - 1
while(min < max) {
val mid = (min / 2) + (max / 2) + 1 // 오버플로우 방지
val value = getValue(mid, N)
// up
if(N < value) { // value < N이 아닌 이유는, 배열 values가 내림차순으로 정렬되어 있기 때문이다.
min = mid + 1
} else if(N == value) {
min = mid;
} else { // value < N
max = mid - 1
}
}
if(getValue(max, N) == N) {
return max;
} else {
return -1;
}
}
// values[cutLength]와 같은 값을 반환함.
fun getValue(cutLength: Int, N: Int): Int {
var cutCableCount = 0
for(originalCableLength : Int in originalCableLengths) {
cutCableCount += originalCableLength / cutLength
}
if(N < cutCableCount) {
return N
} else {
return cutCableCount
}
}'문제 풀이 > 탐색ㆍ그래프' 카테고리의 다른 글
| [백준] 10026 (적록색약) (1) | 2024.11.27 |
|---|---|
| [백준] 14940 (쉬운 최단거리) (1) | 2024.11.13 |
| [백준] 1260 (DFS와 BFS) (0) | 2024.09.24 |
| [백준] 2805 (나무 자르기) (0) | 2024.03.06 |
| [백준] 1920 (수 찾기) (0) | 2023.12.25 |