Keep the Experience Natural, Easy, Light

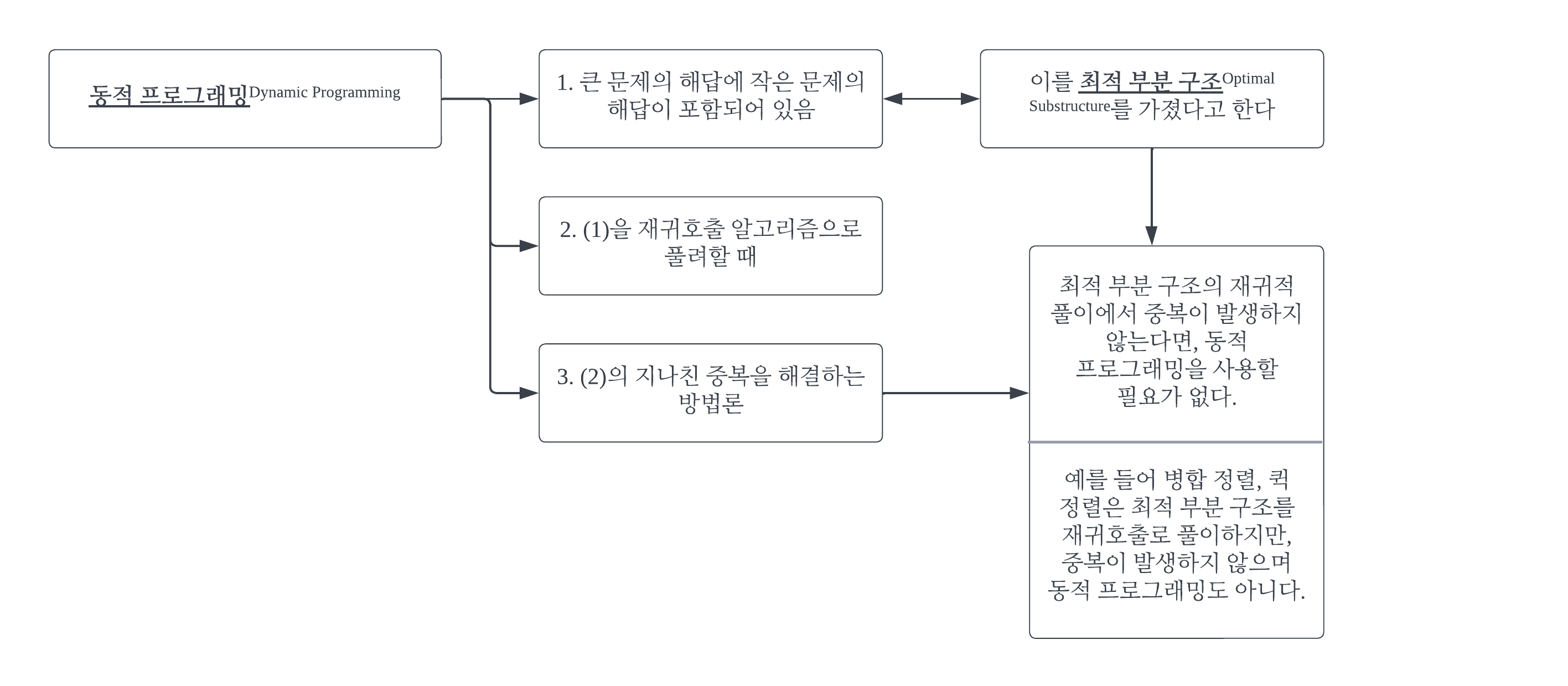
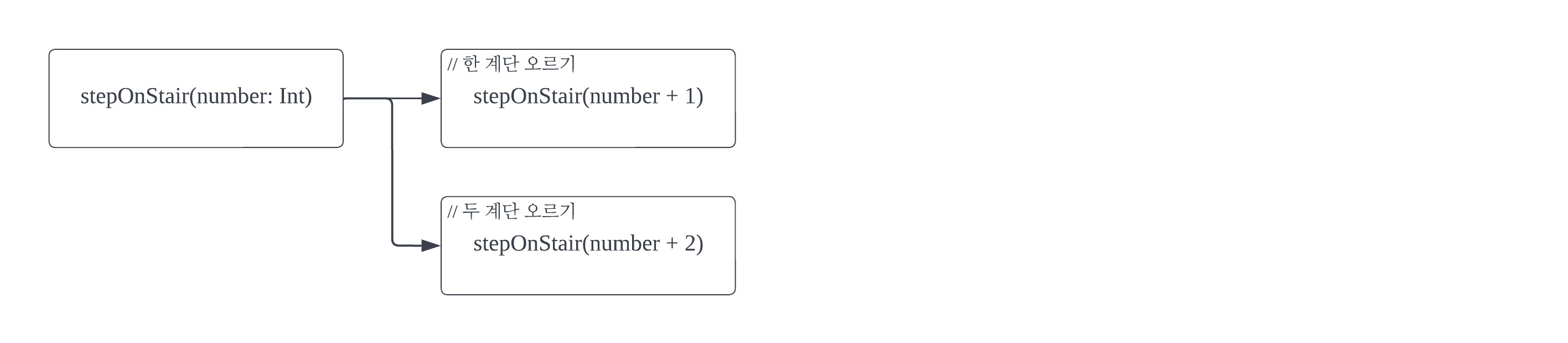
#1 알고리즘#1-1 정의동적 프로그래밍을 한 줄 요약하면 중복의 제거다. 정적(static)이라는 개념과 반대되는 개념으로서, 동적(dynamic)이라는 단어가 이름에 붙었다. 확실히 static이 붙을 만한 작업은 아니지만, 그렇다고 많은 단어들 중에 굳이 dynamic가 붙을 필요 또한 없다. '동적', ' dynamic'이라는 이름은 동적 프로그래밍의 (중복의 제거라는) 핵심을 직관적으로 이해하지 못하게 만든다. 하지만, 관례적으로 이미 굳어진 이름이라 앞으로도 쓰일 것이라는 사실은 안타까우면서도 분명하다. #1-2 종류동적 프로그래밍은 이와 같이 2가지 방식으로 나뉜다. #1-3 상향식(Bottom-up) 접근 [백준] 17626 - Four Squares#1 알고리즘 123 123 재귀 함수가..

#1 알고리즘#1-1 17626번 문제의 함정n이 18인 경우를 예로 든다. 경우 a보다 b의 '제곱수 합의 최소 갯수'가 더 작다. 즉, 무작정 제곱수의 밑을 큰 수로 둔다고 그게 반드시 정답인 것은 아니다. #1-2 점화식x의 제곱수 합의 최소 갯수를 반환하는 함수 f(x)를 가정한다. 이러면, a와 b 각각의 42와 32를 f(x)에 넣으면 f(42) = 1이고 f(32) = 1이다. 즉, 모든 빨간 부분은 f(x)에 넣으면 1로 그 값이 같다. 여기에서 f(x) = 1 + f(y)라는 식을 도출할 수 있다. y값은 a의 경우 18 - 42, b의 경우 18 - 32, c의 경우 18 - 22다. 이를 일반화하면 f(x) = 1 + f(x - i2)다. i의 범위는 1 ~ (x의 제곱근을 넘지 않는..

#1 알고리즘#1-1 병합 정렬 (Merge Sort)#1 알고리즘 병합 정렬의 총 비교 횟수는, 최악의 경우 nlog2n이다 #2 코드 (자바) public static void mergeSort(int[] array, int startIndex, int endIndex) { // (startIndex kenel.tistory.com우선 손님 별 돈을 인출하는 시간들을 정렬해야 한다. 이 문제에서는 병합 정렬을 사용했다. #1-21번 열 + 2번 열 + 3번 열 + ... + personCount번 열로 모든 손님들의 대기 시간 총합을 구한다. #2 코드 - 코틀린fun main() { val personCount = readln().toInt() val timeStrings = re..

#1 알고리즘먼저, 모든 배추에 번호 0을 부여한다. 그리고 배추들을 순회하며 해당 배추의 번호가 0이면 1부터 시작하는 번호를 부여한다. 번호가 부여된 배추는 자신을 기준으로 동, 서, 남, 북에 있는 번호가 0인 배추에 같은 번호를 전달한다. 그리고 전달된 배추 또한 재귀적으로 동, 서, 남, 북에 같은 번호를 전달한다. 같은 번호가 부여된 배추를 하나의 '배추 그룹'으로 생각한다. 여러 개의 '배추 그룹'에 부여된 번호 중 가장 큰 것을 출력하면 그것이 곧 지렁이의 최소 마릿수다.  #2 코드 - 코틀린/* count = 갯수 * number = 번호 */lateinit var cabbageMap : HashMap, Int>fun main() { val testCaseCount = readln..

#1 코드 - 코틀린import java.util.Stackfun main() {    val testCaseCount = readln().toInt()    for(i : Int in 0.. = Stack()    for(char in testCase) {        if(char == '(') {            stack.push('(')        } else { // char == ')'            if(stack.isEmpty()) {                return false            }            stack.pop()        }    }    return stack.isEmpty()}'('을 만나면 스택에 push하고, ')'을 만나면 스택을..

#1 알고리즘#1-1 동적 프로그래밍 (Dynamic Programming), 상향식(Bottom-up) 및 하향식(Top-down) 접근#1 알고리즘 동적 프로그래밍을 한 줄 요약하면 중복의 제거다. 정적(static)이라는 개념과 반대되는 개념으로서, 동적(dynamic)이라는 이름을 붙었다. 확실히 static이 붙을 만한 작업은 아니지만, 그kenel.tistory.com상향식 동적 프로그래밍을 구현해 풀었다. 이 문제에서 가장 핵심적인 부분은 점화식을 구하는 것이다. 나는 먼저 점화식 calculateCombination(sum) = calculateCombination(sum - 1) + calculateCombination(sum - 2) + calculateCombination(sum - ..

#1 알고리즘#1-1 입력 읽기N개의 행과 M개의 열을 가진 2차원 배열 blockHeights를 선언한다. blockHeights 각 원소의 값에는 해당 위치의 높이를 할당한다. #1-2 문제풀이 개요땅이 고른 상태의 블록 갯수는 0, (N*M), (N*M)*1, (N*M)*2, (N*M)*3, ..., (N*M)*256 중 하나다. 이 중에서, (현재 놓여진 블록의 갯수) + (인벤토리 속 블록의 갯수)보다 작거나 같은 갯수들 중 최대값인 갯수를 구한다.그 갯수를 (N*M)로 나누면, 땅을 고르게 만들 수 있는 최대 높이가 된다. 0부터 해당 높이까지의 정수 범위를 내림차순으로 순회(인덱스 i)한다. 내림차 순인 이유는 문제의 조건에서, 같은 소요 시간일때는 더 큰 높이를 정답으로 제출하라고 했기 때..

#1 알고리즘#1-2계단을 오르는 사람 입장에선, 땅에서부터 시작해 1칸 또는 2칸을 오르는 선택지만이 존재한다. 따라서 위와 같은 재귀함수의 형태를 잡을 수 있다.  #1-2또, 문제의 조건에서 밟은 계단이 3연속되면 안된다고 했으므로 해당 조건을 고려해 과 같이 구조를 짤 수 있다. #1-3하지만, stepOnStair()는 재귀호출을 2번 하므로 계단이 많아지면 처리량이 매우 커져버린다. 따라서, 재귀호출 과정에서 가지치기를 할 필요가 있다. 경우 a와 경우 b를 비교해보면, 4번 계단에서 b가 a보다 더 큰 점수를 가진다. 2579번 문제는 마지막 계단까지 누적된 최고 점수를 구하는 것이기에, 경우 b가 존재하는 이상 경우 a와 a에서 파생될 수 많은 경우의 수는 계산할 필요가 없다.또, 경우 b..

#1 알고리즘 #2 코드 - 코틀린fun main() { readln() // 컴퓨터의 갯수는 풀이에 사용하지 않는다. val connectionCount = readln().toInt() val connections : ArrayList> = ArrayList() for(i : Int in 0.. = ArrayList() recursiveFindNextHost(connections, 1, virusHosts) println(virusHosts.size - 1) // 1번 컴퓨터 제외}fun recursiveFindNextHost(connections : ArrayList>, computerNumber : Int, virusHosts : ArrayList) { vir..

#1 알고리즘#1-1 이진 탐색 (Binary search)#1 알고리즘 #1-1 #1-2 이렇게 해서 x의 인덱스 i를 찾으면 좋겠지만, 이 x가 배열 values 어디에도 존재하지 않는 경우도 있을 것이다. 이 경우엔 어떻게 처리해야 할까? #1-3 업 앤 다운 게임은 우리나kenel.tistory.com시간 초과가 뜨지 않게 하기 위해서 배열에 이진 탐색을 수행한다.  #1-2 힙 정렬 (Heap Sort)#1 알고리즘 #1-1 힙(heap)이라는 영어 단어의 사전적 의미는 쌓아 놓은 무더기다. 그리고 이 단어는 프로그래밍에서도 사용된다. 첫째로 메모리 영역에서, 둘째로 자료구조에서다. 이 둘은 서로 다kenel.tistory.com이진 탐색을 수행하려면 먼저, 배열이 정렬되어있어야 한다. 나는 이..