Keep the Experience Natural, Easy, Light

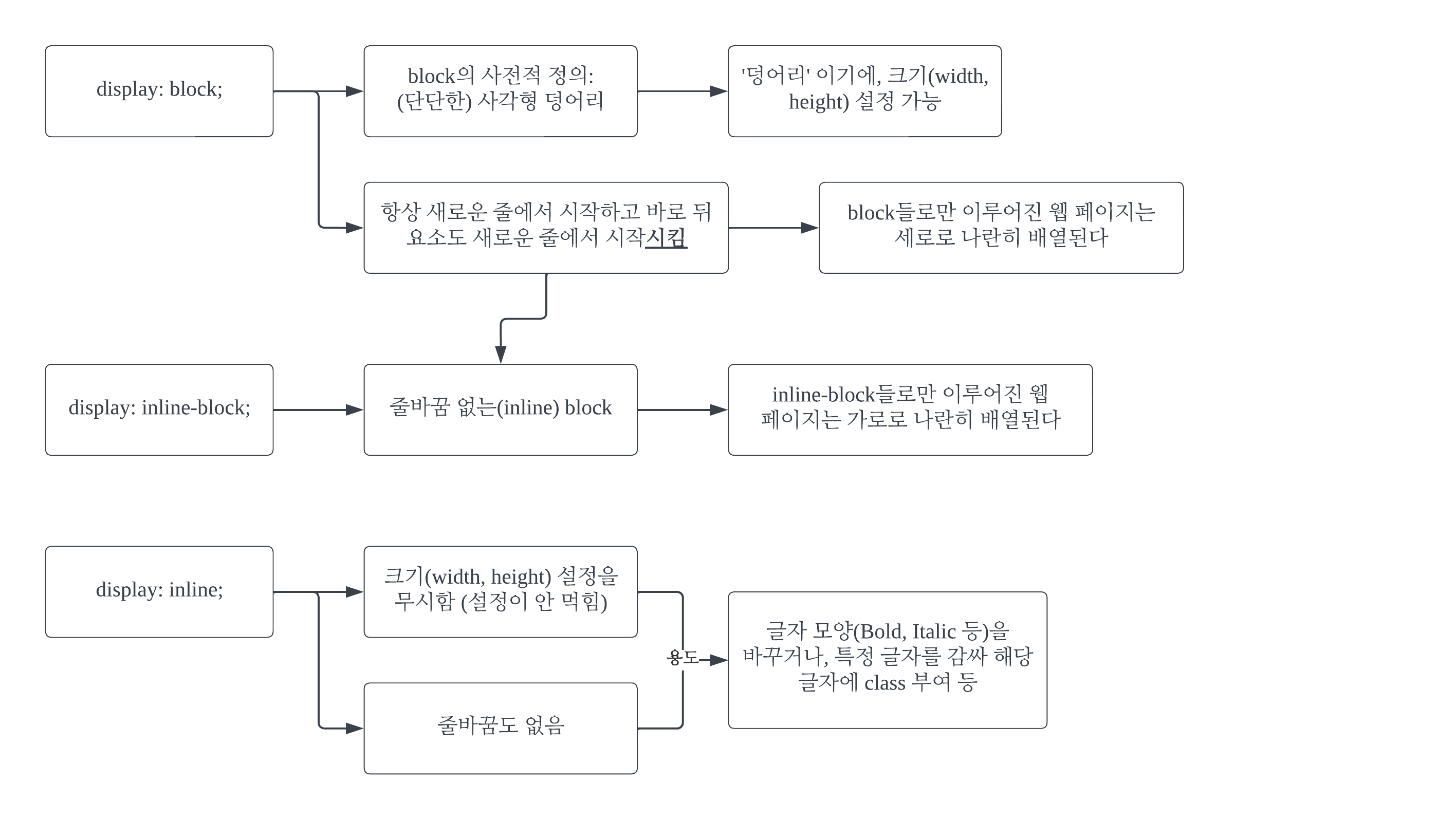
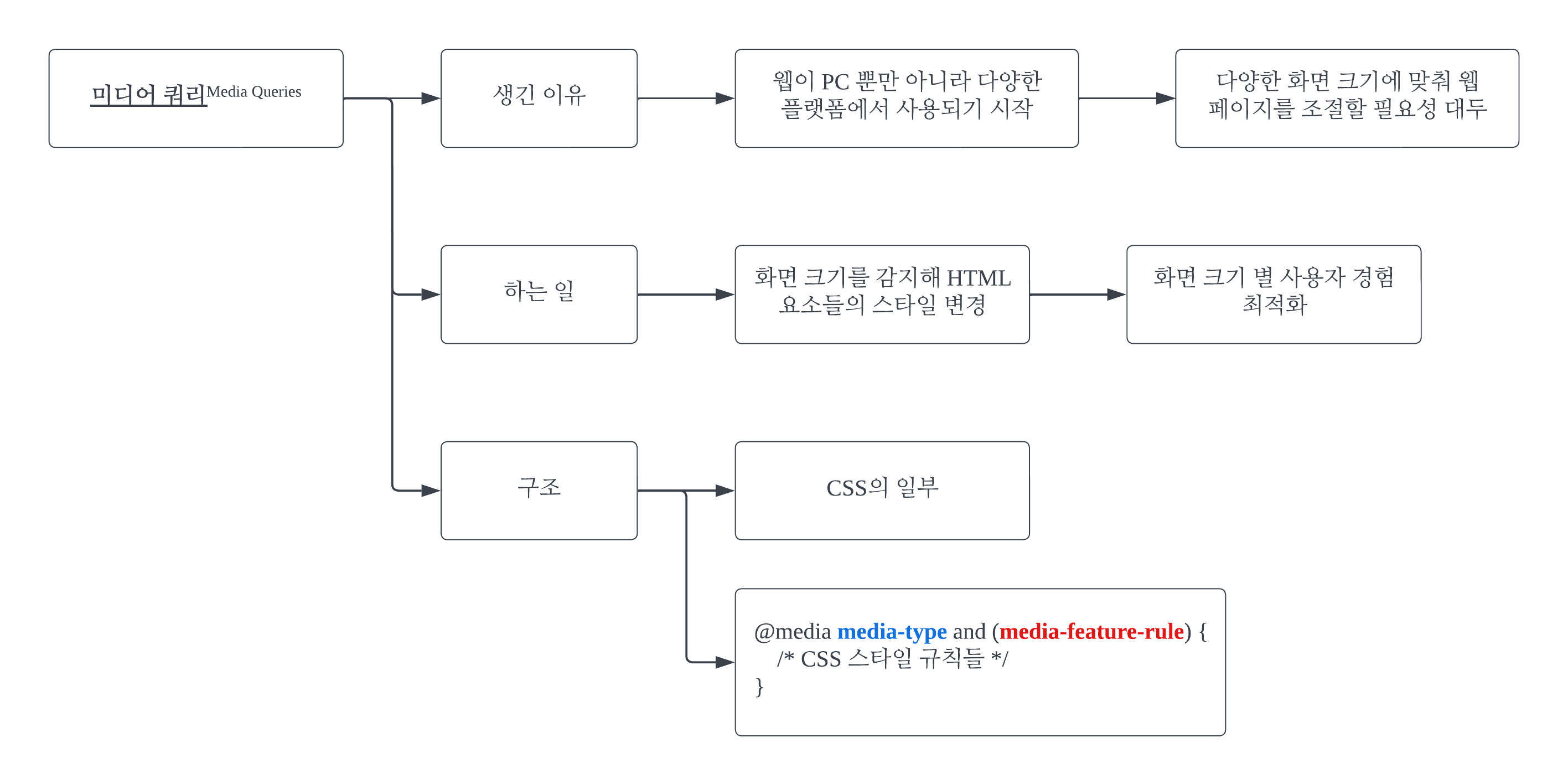
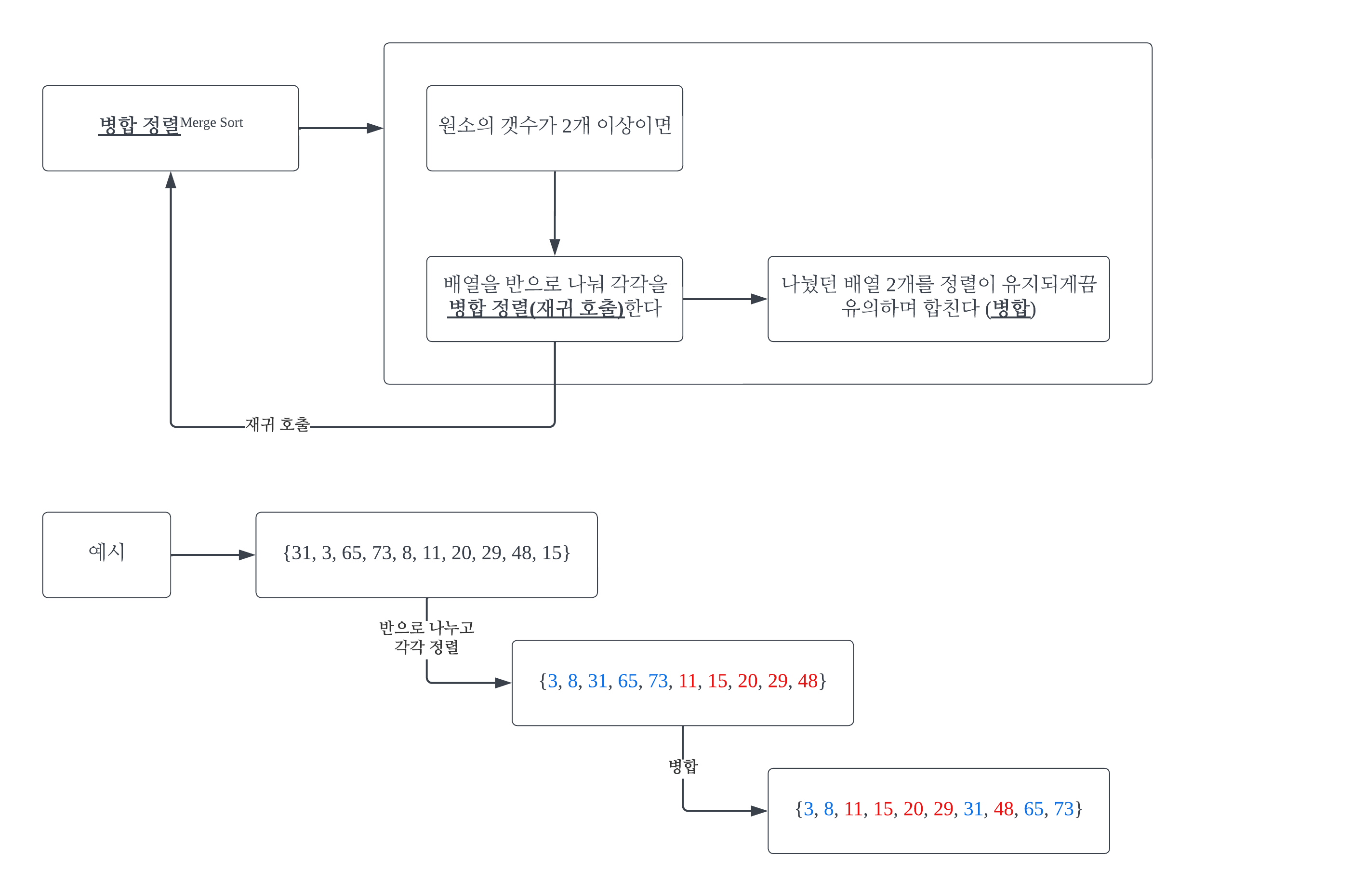
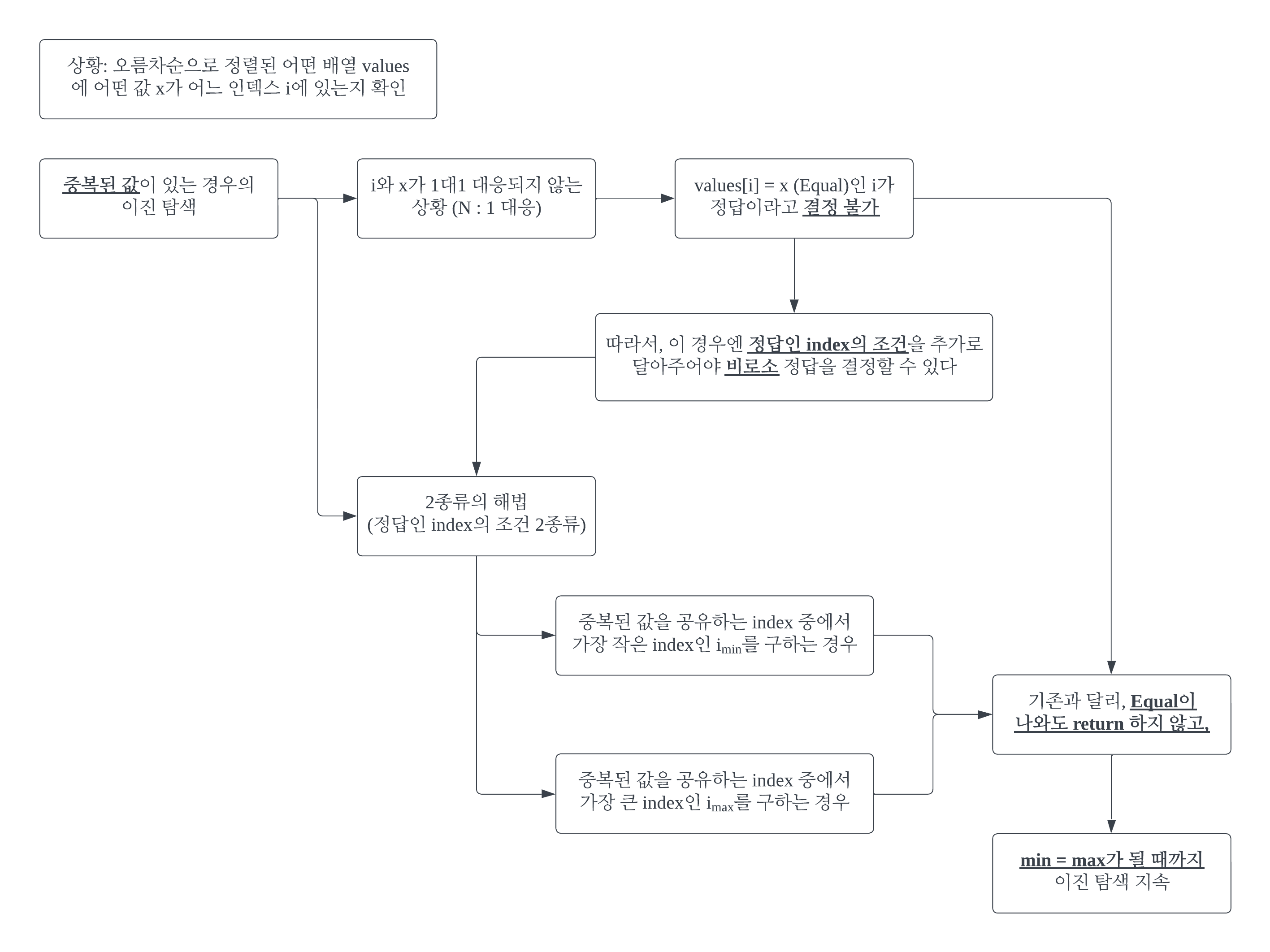
#1 웹 페이지 뒤에 나올 모든 코드를 하나의 파일에 합쳐 넣었다. 백문이 불여일견. 여러 개의 div를 나열하고 각각의 displayㆍwidthㆍheight 스타일 속성을 동적으로 변경할 수 있는 프로그램을 만들었다. 장난감처럼 마음대로 다루어보면서 감을 익히자. #2 알고리즘 #3 코드 #3-1 HTML abcd efgh ijkl mnop qrst uvwx yz #3-2 CSS #display_panels * { /* css iniciation */ padding: 0; margin: 0; box-sizing: border-box; } #display_panels {height: 200px;} #abcd {background-color: aquamarine;} #efgh {background-colo..

#1 알고리즘#1-1어떤 원소를 기준으로 잡을 것이냐는 아무래도 상관없다. 여기에서는 각 배열의 맨 끝 원소를 기준으로 잡기로 한다.

혹시라도 기준을 대략적으로라도 원소들의 평균값에 가깝게 잡을 수 있는 조건이 존재한다면, 해당 조건을 이용해 기준을 잡게끔 응용할 수도 있을 것이다. 기준이 평균값에 가깝게 잡힐수록, 퀵 정렬의 성능이 좋아지기 때문이다. #1-2이 '분할(partition)'의 결과로 기준 원소의 자리가 최종적으로 결정되면, 그 원소는 앞으로의 모든 qucikSort() 재귀 호출에서 사용되지 않고 영원히 그 자리가 고정된다. 즉, 분할 한 번에 원소 하나가 정렬되는 것이다. #1-3 퀵 정렬 - 위키백과, 우리 모두의 백과사전위키백과, 우리 모두의 백과사전. 퀵 정렬(Quicksort..

#1 알고리즘#1-1 #1-2 #2 코드#2-1 자바public static void insertionSort(int[] array, int startIndex, int endIndex) { for(int maxIndex = (startIndex + 1); maxIndex = insertionDestination; i--) { array[i + 1] = array[i]; } array[insertionDestination] = temp;} #2-2 코틀린fun insertionSort(array: Array, startIndex : Int, endIndex : Int) { for(maxIndex : Int in (startIndex + 1)..endIndex) { ..

#1 알고리즘#1-1화면 크기의 다양성을 고려한다는 말이 꼭 다른 플랫폼끼리의 다양성만을 의미하진 않는다. PC에서 웹 페이지를 볼 때 인터넷 창을 최대화해서 보지 않고, 예를 들면 화면 좌우 각각에 폭을 줄인 인터넷 창을 하나씩 켜 놓은 경우가 있다. 이때, 그에 맞는 적절한 동작을 미디어 쿼리가 수행할 수 있다. #1-2 #2 코드#2-1 HTML Media Queries #2-2 CSS@media screen and (max-width: 767px) { /* width

#1 알고리즘#1-1힙(heap)이라는 영어 단어의 사전적 의미는 쌓아 놓은 무더기다. 그리고 이 단어는 프로그래밍에서도 사용된다. 첫째로 메모리 영역에서, 둘째로 자료구조에서다. 이 둘은 서로 다른 개념이지만, 힙(heap)이라는 단어를 쓴 만큼 각각 힙의 사전적 의미와 관련된 내용이 있다. 메모리 영역에서의 힙은 무더기라는 뉘앙스를 풍긴다. 프로그램 수행 도중 그 크기가 변하지 않는 정적 할당과 달리 동적 할당은 필요한 만큼 크기가 무더기로 증가할 수 있기 때문이다. 자료구조에서의 힙은 '무더기'기 보단, 쌓임이라는 의미가 강조된다. 노드가 특정한 규칙을 지키며 차곡차곡 쌓이는 모습에서 힙이라는 이름이 붙었다. #1-2힙 정렬은 자료구조에서의 힙을 이용하는 정렬이다. 자료구조에서의 힙은 최소 힙과 최..

#1 알고리즘#1-1 #1-2 #1-3 #1-4 #1-5병합 정렬의 총 비교 횟수는, 최악의 경우 nlog2n이다 #2 코드#2-1 자바public static void mergeSort(int[] array, int startIndex, int endIndex) { // (startIndex  #2-2 코틀린fun mergeSort(array: Array, startIndex : Int, endIndex : Int) { // (startIndex , startIndex: Int, midIndex : Int, endIndex: Int) { // array에서 나뉜 'f'irst 부분을 순회할 인덱스 f var f = startIndex // f의 최댓값은 midIndex // ..

#1 알고리즘#1-1정렬 방식이 마치 거품이 수중에 있다가 수면 위로 보글보글 올라가는 모습과 비슷해서 버블 정렬이라고 이름 붙여졌다. 기본적인 버블 정렬은, 정렬 작업을 시작할 때 중간에 배열 이미 정렬된 상태여도 maxIndex가 1이 되는 마지막 반복까지 무의미한 순환을 계속한다. 이 문제점을 해결하기 위해 알고리즘에 한 가지 장치를 할 수 있는데, 그걸 향상된 버블 정렬이라고 부른다. #2-1반드시 n * (n - 1) / 2번의 비교를 하는 일반 버블 정렬에 비해, 향상된 버블 정렬은 비교 횟수를 최소 (n - 1)번까지 낮출 수 있다. #2 코드#2-1 자바public static void bubbleSort(int[] array, int startIndex, int endIndex) { ..

#1 알고리즘#1-1 이진 탐색 (Binary search)#1 알고리즘 이렇게 해서 x의 인덱스 i를 찾으면 좋겠지만, 이 x가 배열 values 어디에도 존재하지 않는 경우도 있을 것이다. 이 경우엔 어떻게 처리해야 할까? 업 앤 다운 게임은 우리나라에선 소주kenel.tistory.com해당 글에서 이어진다. #1-2 #1-3중복된 값이 없는 경우의 이진 탐색에선 min 있는 경우의 이진 탐색에선 min = max가 되는 시점이 while의 탈출 시점이다. min = max는 검색 범위가 i에 최대로 접근 즉, 아예 같은 값이 되었다는 의미다. #1-4binarySearch() 대비 binarySearchFirstIndex() 또는 binarySearchLastIndex()에서 다른 부분을 빨갛게 ..

#1 알고리즘 #1-1 #1-2 이렇게 해서 x의 인덱스 i를 찾으면 좋겠지만, 이 x가 배열 values 어디에도 존재하지 않는 경우도 있을 것이다. 이 경우엔 어떻게 처리해야 할까? #1-3 업 앤 다운 게임은 우리나라에선 소주병 뚜껑에 적혀 있는 0 ~ 50 사이의 정수를 가지고 맞추는 술 게임의 이미지가 강하다. 어떤 상황을 가정해보겠다. 어느 병뚜껑엔 알 수 없는 이유로 34.5라는 정수가 아닌 수가 적혀 있었다. 사회자는 병뚜껑에 쓰인 숫자를 보고 당황했지만, 장난기가 발동해 그냥 게임을 진행해 보기로 했다. 참여자들은 병뚜껑에 쓰인 숫자가 정수가 아닐 거라고는 생각지 못하고 업 앤 다운 게임에 임할 것이다. 이 업 앤 다운 게임은 실패할 운명이다. 하지만, 이 사례를 상상해 보면서 이진 탐색..

#1 알고리즘#1-1 #1-2 #2 코드#2-1 자바public static void selectionSort(int[] array, int startIndex, int endIndex) { for(int maxIndex = endIndex; startIndex  #2-2 코틀린fun selectionSort(array: Array, startIndex : Int, endIndex : Int) { for(maxIndex : Int in endIndex downTo (startIndex + 1)) { // 배열을 순회하며 가장 값이 큰 원소의 index를 구한다 var indexOfLargest = startIndex; for(i : Int in (s..